fzero (MATLAB Function Reference)

Zero of a function of one variable

z = fzero('fun',x)
z = fzero('fun',x,tol)
z = fzero('fun',x,tol,trace)
z = fzero('fun',x,tol,trace,P1,P2,...)

Description

fzero('fun',x)

finds a zero of fun. fun is a string containing the name of a real-valued function of a single real variable. The value returned is near a point where fun changes sign, or NaN if the search fails.

fzero('fun',x)

where x is a vector of length 2, assumes x is an interval where the sign of f(x(1)) differs from the sign of f(x(2)). An error occurs if this is not true. Calling fzero with an interval guarantees fzero will return a value near a point where fun changes sign.

fzero('fun',x)

where x is a scalar value, uses x as a starting point. fzero looks for an interval containing a sign change for fun and containing x. If no such interval is found, NaN is returned. In this case, the search terminates when the search interval is expanded until an Inf, NaN, or complex value is found.

fzero('fun',x,tol)

returns an answer accurate to within a relative error of tol.

z = fzero('fun',x,tol,trace)

displays information at each iteration.

z = fzero('fun',x,tol,trace,P1,P2,...)

provides for additional arguments passed to the function fun(x,P1,P2,...). Pass an empty matrix for tol or trace to use the default value, for example: fzero('fun',x,[],[],P1)

For the purposes of this command, zeros are considered to be points where the function actually crosses, not just touches, the x-axis.

Arguments




fun

A string containing the name of a file in which an arbitrary function of one variable is defined.


x

Your initial estimate of the x-coordinate of a zero of the function or an interval in which you think a zero is found. 


tol

The relative error tolerance. By default, tol is eps.


trace

A nonzero value that causes the fzero command to display information at each iteration of its calculations. 


P1,P2

Additional arguments passed to the function

`fun`	A string containing the name of a file in which an arbitrary function of one variable is defined.
`x`	Your initial estimate of the x-coordinate of a zero of the function or an interval in which you think a zero is found.
`tol`	The relative error tolerance. By default, tol is `eps`.
`trace`	A nonzero value that causes the `fzero` command to display information at each iteration of its calculations.
`P1,P2`	Additional arguments passed to the function

Examples

Calculate

by finding the zero of the sine function near 3.

x = fzero('sin',3)
x =
    3.1416

To find the zero of cosine between 1 and 2:

x = fzero('cos',[1 2])
x =

1.5708

Note that cos(1) and cos(2) differ in sign.

To find a zero of the function: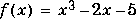

write an M-file called f.m.

function y = f(x)
y = x.^3-2*x-5;

To find the zero near 2

z = fzero('f',2)
z =
    2.0946

Since this function is a polynomial, the statement roots([1 0 -2 -5]) finds the same real zero, and a complex conjugate pair of zeros.

    2.0946
   -1.0473 + 1.1359i
   -1.0473 - 1.1359i

fzero('abs(x)+1', 1) returns NaN since this function does not change sign anywhere on the real axis (and does not have a zero as well).

Algorithm

The fzero command is an M-file. The algorithm, which was originated by T. Dekker, uses a combination of bisection, secant, and inverse quadratic interpolation methods. An Algol 60 version, with some improvements, is given in [1]. A Fortran version, upon which the fzero M-file is based, is in [2].

Limitations

The fzero command defines a zero as a point where the function crosses the x-axis. Points where the function touches, but does not cross, the x-axis are not valid zeros. For example, y = x.^2 is a parabola that touches the x-axis at (0,0). Since the function never crosses the x-axis, however, no zero is found. For functions with no valid zeros, fzero executes until Inf, NaN, or a complex value is detected.