This display and interface will allow you to do everything that anyone in class can do with
with the EULR program for the TI-86. Before explaining how to use the interface, let me tell
you what each part of the interface does.
Below are a bunch of informational items. Those items in red are
essential to working with this applet. The others are just incidental; read them only if you
are curious.
The function input
The bottom half of this viewing is the input interface. At the top of the imput fields is
this field:
(Oops, you can see part of my cursor.) This is where you would put your differential equation.
For example, if you were studying the model for the population of California Sea Lions, you
would change the x2-y2 that should be in the interface field to 0.092*y.
You can change this function to whatever you want, and you can use both the x and y variables.
Viewing Rectangle
The next interface fields determine the dimensions of yoru viewing rectangle.
What effect these inputs have on your display should be obvious. If it's not, you should notice
that the viewing rectangle that first appears in the browser window covers the area -1.0
< x < 1.0 and -1.0 < y < 1.0.
You can change this viewing rectangle's dimensions to whatever you want.
Step size and Initial Condition
The last thing interfaces you'll need to play with are those that set your step size (VERY
important in Euler's method) and the coordinates of the point on your solution curve (what
I call, above, your initial conditions). To set these, look for the Step Size interface field
to the right of the "Submit All" button. It's small and looks like this:
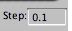The intial conditions are set near the bottom of the interface.
The "Submit" button, here, only submits a new initial condition if you changed it.
The "Show Table" button creates a table of values for the function you are estimating
using Euler's method. The table should appear in an external window. it contains three columns
of numbers: the step taken, the x value at that step, and the y value at that step.
Committing your modifications
When you have made all the changes you want to make in the interface, you need to tell the applet
to start computing. To do this, hit the 
button.
Number of segments
This number here isn't really important to what we want to use this applet for, but I'll tell
it's story, anyway.
You can see in the viewing rectangle lots of blue line segments. These represent the tangent
lines determined by the expression for dy/dx. The number that goes into this interface field
determines how many of these tange line segments you see. There's no need to mess with it,
really, but go ahead and play with it if you like.
