viewmtx (MATLAB Function Reference)

View transformation matrices

T = viewmtx(az,el)
T = viewmtx(az,el,phi)
T = viewmtx(az,el,phi,xc)

Description

viewmtx

computes a 4-by-4 orthographic or perspective transformation matrix that projects four-dimensional homogeneous vectors onto a two-dimensional view surface (e.g., your computer screen).

T = viewmtx(az,el)

returns an orthographic transformation matrix corresponding to azimuth az and elevation el. az is the azimuth (i.e., horizontal rotation) of the viewpoint in degrees. el is the elevation of the viewpoint in degrees. This returns the same matrix as the commands

view(az,el)
T = view

but does not change the current view.

T = viewmtx(az,el,phi)

returns a perspective transformation matrix. phi is the perspective viewing angle in degrees. phi is the subtended view angle of the normalized plot cube (in degrees) and controls the amount of perspective distortion:


Phi	Description
0 degrees	Orthographic projection
10 degrees	Similar to telephoto lens
25 degrees	Similar to normal lens
60 degrees	Similar to wide angle lens

You can use the matrix returned to set the view transformation with view(T). The 4-by-4 perspective transformation matrix transforms four-dimensional homogeneous vectors into unnormalized vectors of the form (x,y,z,w), where w is not equal to 1. The x- and y-components of the normalized vector (x/w, y/w, z/w, 1) are the desired two-dimensional components (see example below).

T = viewmtx(az,el,phi,xc)

returns the perspective transformation matrix using xc as the target point within the normalized plot cube (i.e., the camera is looking at the point xc). xc is the target point that is the center of the view. You specify the point as a three-element vector, xc = [xc,yc,zc], in the interval [0,1]. The default value is xc = [0,0,0].

Remarks

A four-dimensional homogenous vector is formed by appending a 1 to the corresponding three-dimensional vector. For example, [x,y,z,1] is the four-dimensional vector corresponding to the three-dimensional point [x,y,z].

Examples

Determine the projected two-dimensional vector corresponding to the three-dimensional point (0.5,0.0,--3.0) using the default view direction. Note that the point is a column vector.

A = viewmtx(--37.5,30);
x4d = [.5  0  --3  1]';
x2d = A*x4d;
x2d = x2d(1:2)
x2d =
     0.3967
    --2.4459

Vectors that trace the edges of a unit cube are

x = [0  1  1  0  0  0  1  1  0  0  1  1  1  1  0  0];
y = [0  0  1  1  0  0  0  1  1  0  0  0  1  1  1  1];
z = [0  0  0  0  0  1  1  1  1  1  1  0  0  1  1  0];

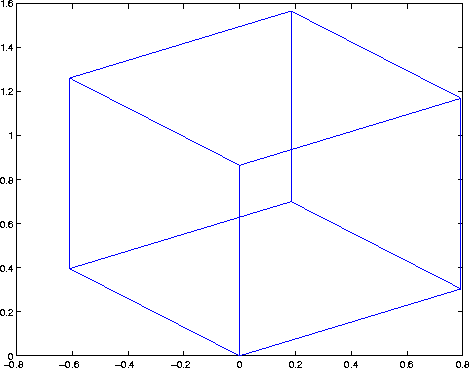
Transform the points in these vectors to the screen, then plot the object:

A = viewmtx(--37.5,30);
[m,n] = size(x);
x4d = [x(:),y(:),z(:),ones(m*n,1)]';
x2d = A*x4d;
x2 = zeros(m,n); y2 = zeros(m,n);
x2(:) = x2d(1,:);
y2(:) = x2d(2,:);
plot(x2,y2)

Use a perspective transformation with a 25 degree viewing angle:

A = viewmtx(--37.5,30,25);
x4d = [.5  0  --3  1]';
x2d = A*x4d;
x2d = x2d(1:2)/x2d(4)   % Normalize
x2d =
     0.1777
    --1.8858

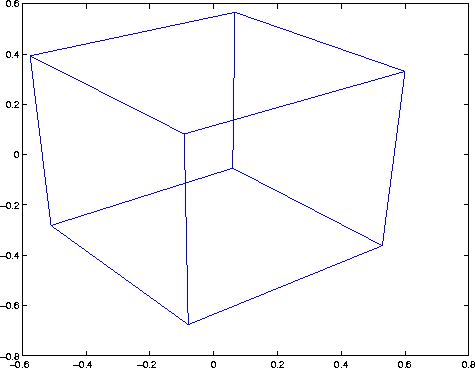
Transform the cube vectors to the screen and plot the object:

A = viewmtx(--37.5,30,25);
[m,n] = size(x);
x4d = [x(:),y(:),z(:),ones(m*n,1)]';
x2d = A*x4d;
x2 = zeros(m,n); y2 = zeros(m,n);
x2(:) = x2d(1,:)./x2d(4,:);
y2(:) = x2d(2,:)./x2d(4,:);
plot(x2,y2)