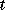 is a scalar independent variable, typically representing time.
is a scalar independent variable, typically representing time.
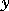 is a vector of dependent variables.
is a vector of dependent variables.
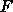 is a function of
is a function of 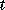 and
and 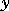 returning a column vector the same length as
returning a column vector the same length as 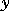 .
.
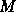 and
and 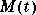 represent nonsingular constant or time dependent mass matrices.
represent nonsingular constant or time dependent mass matrices.
| MATLAB Function Reference | Search Help Desk |
| odefile | Examples See Also |
Define a differential equation problem for ODE solvers
odefile is not a command or function. It is a help entry that describes how to create an M-file defining the system of equations to be solved. This definition is the first step in using any of MATLAB's ODE solvers. In MATLAB documentation, this M-file is referred to as odefile, although you can give your M-file any name you like.
You can use the odefile M-file to define a system of differential equations in one of these forms: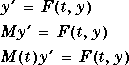
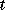 is a scalar independent variable, typically representing time.
is a scalar independent variable, typically representing time.
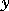 is a vector of dependent variables.
is a vector of dependent variables.
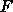 is a function of
is a function of 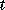 and
and 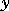 returning a column vector the same length as
returning a column vector the same length as 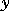 .
.
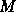 and
and 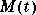 represent nonsingular constant or time dependent mass matrices.
represent nonsingular constant or time dependent mass matrices.
t and y, although it does not have to use them. By default, the ODE file must return a column vector the same length as y.
Only the stiff solvers ode15s, ode23t, and ode23tb can solve 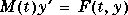 .
. ode15s, ode23s, ode23t, and ode23tb can solve equations of the form 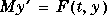 .
Beyond defining a system of differential equations, you can specify an entire initial value problem (IVP) within the ODE
.
Beyond defining a system of differential equations, you can specify an entire initial value problem (IVP) within the ODE M-file, eliminating the need to supply time and initial value vectors at the command line (see Examples on page 2-517).
help odefile to display the help entry.
switch flag
case '' % Return dy/dt = f(t,y).
varargout{1} = f(t,y,p1,p2);
case 'init' % Return default [tspan,y0,options].
[varargout{1:3}] = init(p1,p2);
case 'jacobian' % Return Jacobian matrix df/dy.
varargout{1} = jacobian(t,y,p1,p2);
case 'jpattern' % Return sparsity pattern matrix S.
varargout{1} = jpattern(t,y,p1,p2);
case 'mass' % Return mass matrix M(t) or M.
varargout{1} = mass(t,y,p1,p2);
case 'events' % Return [value,isterminal,direction].
[varargout{1:3}] = events(t,y,p1,p2);
otherwise
error(['Unknown flag ''' flag '''.']);
end
% -------------------------------------------------------------
function dydt = f(t,y,p1,p2)
dydt = < Insert a function of t and/or y, p1, and p2 here. >
% -------------------------------------------------------------
function [tspan,y0,options] = init(p1,p2)
tspan = < Insert tspan here. >;
y0 = < Insert y0 here. >;
options = < Insert options = odeset(...) or [] here. >;
% ------------------------------------------------------------
function dfdy = jacobian(t,y,p1,p2)
dfdy = < Insert Jacobian matrix here. >;
% ------------------------------------------------------------
function S = jpattern(t,y,p1,p2)
S = < Insert Jacobian matrix sparsity pattern here. >;
% ------------------------------------------------------------
function M = mass(t,y,p1,p2)
M = < Insert mass matrix here. >;
% ------------------------------------------------------------
function [value,isterminal,direction] = events(t,y,p1,p2)
value = < Insert event function vector here. >
isterminal = < Insert logical ISTERMINAL vector here.>;
direction = < Insert DIRECTION vector here.>;
t and y vectors from the ODE solvers and must
return a column vector the same length as y. The optional input argument
flag determines the type of output (mass matrix, Jacobian, etc.) returned
by the ODE file.
switch statement determines the type of output required, so that the
ODE file can pass the appropriate information to the solver. (See steps 4 - 9.)
'init') case, the ODE file returns basic
information (time span, initial conditions, options) to the solver. If you omit
this case, you must supply all the basic information on the command line.
'jacobian' case, the ODE file returns a Jacobian matrix to the
solver. You need only provide this case when you wish to improve the
performance of the stiff solvers ode15s and ode23s.
'jpattern' case, the ODE file returns the Jacobian sparsity pattern
matrix to the solver. You need provide this case only when you want to
generate sparse Jacobian matrices numerically for a stiff solver.
'mass' case, the ODE file returns a mass matrix to the solver. You
need provide this case only when you want to solve a system in either of the
forms 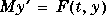 or
or 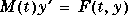 .
.
'events' case, the ODE file returns to the solver the values that it
needs to perform event location. When the Events property is set to 1, the
ODE solvers examine any elements of the event vector for transitions to,
from, or through zero. If the corresponding element of the logical
isterminal vector is set to 1, integration will halt when a zero-crossing is
detected. The elements of the direction vector are -1, 1, or 0, specifying
that the corresponding event must be decreasing, increasing, or that any
crossing is to be detected. See Using MATLAB and also the examples
ballode and orbitode.
flag generates an error.
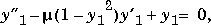
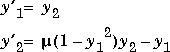 The M-file
The M-file
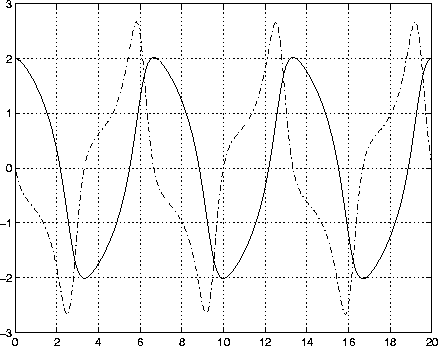
function out1 = vdp1(t,y) out1 = [y(2); (1-y(1)^2)*y(2) - y(1)];defines this system of equations (with µ = 1). To solve the van der Pol system on the time interval
[0 20] with initial values (at time 0) of y(1) = 2 and y(2) = 0, use:
[t,y] = ode45('vdp1',[0 20],[2; 0]);
plot(t,y(:,1),'-',t,y(:,2),'-.')
To specify the entire initial value problem (IVP) within the M-file, rewrite vdp1 as follows:
functionYou can now solve the IVP without entering any arguments from the command line:[out1,out2,out3]=vdp1(t,y,flag) if nargin < 3 | isempty(flag) out1=[y(1).*(1-y(2).^2)-y(2);y(1)]; else switch(flag) case 'init' % Return tspan, y0 and options out1 = [0 20]; out2 = [2; 0]; out3 = []; otherwise error(['Unknown request ''' flag '''.']); end end
[T,Y] = ode23('vdp1')
In this example the ode23 function looks to the vdp1 M-file to supply the missing arguments. Note that, once you've called odeset to define options, the calling syntax:
[T,Y] = ode23('vdp1',[],[],options)
also works, and that any options supplied via the command line override corresponding options specified in the M-file (see odeset).
Some example ODE files we have provided include b5ode,brussode,vdpode,orbitode, and rigidode. Use type filename from the MATLAB command line to see the coding for a specific ODE file.
The Applying MATLAB and the reference entries for the ODE solvers and their associated functions:
ode23, ode45, ode113, ode15s, ode23s, odeget, odeset