besseli, besselk (MATLAB Function Reference)

Modified Bessel functions

I = besseli(nu,Z)     Modified Bessel function of the 1st kind
K = besselk(nu,Z)     Modified Bessel function of the 3rd kind
E = besseli(nu,Z,1)
K = besselk(nu,Z,1)
[I,ierr] = besseli(...)
[K,ierr] = besselk(...)

Definitions

The differential equation

where

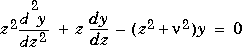
is a nonnegative constant, is called the modified Bessel's equation, and its solutions are known as modified Bessel functions.

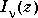and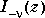

form a fundamental set of solutions of the modified Bessel's equation for noninteger

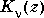is a second solution, independent of

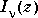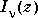and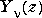

are defined by: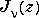

Description

I = besseli(nu,Z)

computes modified Bessel functions of the first kind,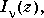

for each element of the array Z. The order nu need not be an integer, but must be real. The argument Z can be complex. The result is real where Z is positive.

If nu and Z are arrays of the same size, the result is also that size. If either input is a scalar, it is expanded to the other input's size.If one input is a row vector and the other is a column vector, the result is a two-dimensional table of function values.

K = besselk(nu,Z)

computes modified Bessel functions of the second kind,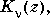

for each element of the complex array Z.

E = besseli(nu,Z,1)

computes besseli(nu,Z).*exp(-Z).

K = besselk(nu,Z,1)

computes besselk(nu,Z).*exp(-Z).

[I,ierr] = besseli(...) and [K,ierr] = besselk(...)

also return an array of error flags.


`ierr = 1`	Illegal arguments.
`ierr = 2`	Overflow. Return `Inf`.
`ierr = 3`	Some loss of accuracy in argument reduction.
`ierr = 4`	Unacceptable loss of accuracy, `Z` or `nu` too large.
`ierr = 5`	No convergence. Return `NaN`.

Examples

besseli(3:9,(0:.2:10)',1) generates the entire table on page 423 of Abramowitz and Stegun, Handbook of Mathematical Functions.

besselk(3:9,(0:.2:10)',1) generates part of the table on page 424 of Abramowitz and Stegun, Handbook of Mathematical Functions.

Algorithm

The besseli and besselk functions use a Fortran MEX-file to call a library developed by D. E. Amos [3] [4].