
| Symbolic Math Toolbox | Search Help Desk | |
| ifourier | See Also |
Inverse Fourier integral transform.
f = ifourier(F) f = ifourier(F,u) f = ifourier(F,v,u)
f = ifourier(F) is the inverse Fourier transform of the scalar symbolic object F with default independent variable w. The default return is a function of x. The inverse Fourier transform is applied to a function of w and returns a function of x.

F = F(x), ifourier returns a function of t.

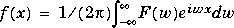
f = ifourier(F,u) makes f a function of u instead of the default x.

u is a scalar symbolic object.
f = ifourier(F,v,u) takes F to be a function of v and f to be a function of u instead of the default w and x, respectively.
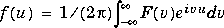
fourier, ilaplace, iztrans