gradient (MATLAB Function Reference)

Numerical gradient

FX = gradient(F)
[FX,FY] = gradient(F)
[Fx,Fy,Fz,...] = gradient(F)
[...] = gradient(F,h)
[...] = gradient(F,h1,h2,...)

Definition

The gradient of a function of two variables, F(x,y), is defined as:

and can be thought of as a collection of vectors pointing in the direction of increasing values of

In MATLAB, numerical gradients (differences) can be computed for functions with any number of variables. For a function of N variables, F(x,y,z,...),

Description

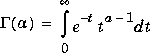
FX = gradient(F)

where F is a vector returns the one-dimensional numerical gradient of F. FX corresponds to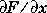

, the differences in the x direction.

[FX,FY] = gradient(F)

where F is a matrix returns the x and y components of the two-dimensional numerical gradient. FX corresponds to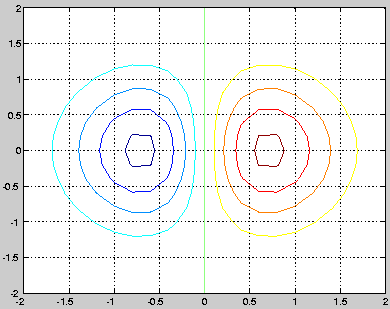

, the differences in the x (column) direction. FY corresponds to

, the differences in the y (row) direction. The spacing between points in each direction is assumed to be one.

[FX,FY,FZ,...] = gradient(F)

where F has N dimensions returns the N components of the gradient of F.

There are two ways to control the spacing between values in F:

A single spacing value, h, specifies the spacing between points in every direction.

N spacing values (h1,h2,...) specify the spacing for each dimension of F. Scalar spacing parameters specify a constant spacing for each dimension. Vector parameters specify the coordinates of the values along corresponding dimensions of F. In this case, the length of the vector must match the size of the corresponding dimension.

[...] = gradient(F,h)

where h is a scalar uses h as the spacing between points in each direction.

[...] = gradient(F,h1,h2,...)

with N spacing parameters specifies the spacing for each dimension of F.

Examples

The statements

v = -2:0.2:2;
[x,y] = meshgrid(v);
z = x .* exp(-x.^2 - y.^2);
[px,py] = gradient(z,.2,.2);
contour(v,v,z), hold on, quiver(px,py), hold off

produce

Given,

F(:,:,1) = magic(3); F(:,:,2) = pascal(3);
gradient(F) takes dx = dy = dz = 1.
[PX,PY,PZ] = gradient(F,0.2,0.1,0.2) takes dx = 0.2, dy = 0.1, and 
dz = 0.2.