| MATLAB Function Reference | Search Help Desk |
| del2 | Examples See Also |
L = del2(U) L = del2(U,h) L = del2(U,hx,hy) L = del2(U,hx,hy,hz,...)If the matrix
U is regarded as a function u(x,y) evaluated at the point on a square grid, then 4*del2(U) is a finite difference approximation of Laplace's differential operator applied to u, that is: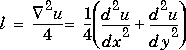
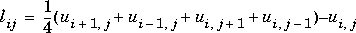
del2(U) is an approximation,
L = del2(U)
where U is a rectangular array is a discrete approximation of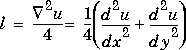 
L is the same size as U with each element equal to the difference between an element of U and the average of its four neighbors.
L = del2(U)
when U is an multidimensional array, returns an approximation of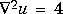
where N is ndims(u).
L = del2(U,h)
where H is a scalar uses H as the spacing between points in each direction (h=1 by default).
L = del2(U,hx,hy)
when U is a rectangular array, uses the spacing specified by hx and hy. If hx is a scalar, it gives the spacing between points in the x-direction. If hx is a vector, it must be of length size(u,2) and specifies the x-coordinates of the points. Similarly, if hy is a scalar, it gives the spacing between points in the y-direction. If hy is a vector, it must be of length size(u,1) and specifies the y-coordinates of the points.
L = del2(U,hx,hy,hz,...)
where U is multidimensional uses the spacing given by hx, hy, hz, ...
The function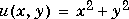
has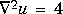
For this function, 4*del2(U) is also 4.
[x,y] = meshgrid(-4:4,-3:3);
U = x.*x+y.*y
U =
25 18 13 10 9 10 13 18 25
20 13 8 5 4 5 8 13 20
17 10 5 2 1 2 5 10 17
16 9 4 1 0 1 4 9 16
17 10 5 2 1 2 5 10 17
20 13 8 5 4 5 8 13 20
25 18 13 10 9 10 13 18 25
V = 4*del2(U)
V =
4 4 4 4 4 4 4 4 4
4 4 4 4 4 4 4 4 4
4 4 4 4 4 4 4 4 4
4 4 4 4 4 4 4 4 4
4 4 4 4 4 4 4 4 4
4 4 4 4 4 4 4 4 4
4 4 4 4 4 4 4 4 4
diff Differences and approximate derivatives
gradient Numerical gradient