fmins (MATLAB Function Reference)

Minimize a function of several variables

x = fmins('fun',x0)
x = fmins('fun',x0,options)
x = fmins('fun',x0,options,[],P1,P2, ...)
[x,options] = fmins(...)

Description

x = fmins('fun',x0)

returns a vector x which is a local minimizer of
fun(x) near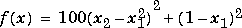

x = fmins('fun',x0,options)

does the same as the above, but uses options control parameters.

x = fmins('fun',x0,options,[],P1,P2,...)

does the same as above, but passes arguments to the objective function, fun(x,P1,P2, ...). Pass an empty matrix for options to use the default value.

[x,options] = fmins(...)

returns, in options(10), a count of the number of steps taken.

Arguments


`x0`	Starting vector.
`P1,P2...`	Arguments to be passed to `fun`.
`[]`	Argument needed to provide compatibility with `fminu` in the Optimization Toolbox.
`fun`	A string containing the name of the objective function to be minimized. `fun(x)` is a scalar valued function of a vector variable.
`options`	A vector of control parameters. Only four of the 18 components of `options` are referenced by `fmins`; Optimization Toolbox functions use the others. The four control `options` used by `fmins` are: `options(1)` -- If this is nonzero, intermediate steps in the solution are displayed. The default value of `options(1)` is 0. `options(2)` and `options(3)` -- These are the termination tolerances for `x` and `function(x)`, respectively. The default values are `1.e-4`. `options(14)` -- This is the maximum number of steps. The default value is `500`.

Examples

A classic test example for multidimensional minimization is the Rosenbrock banana function:

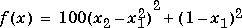
The minimum is at (1,1) and has the value 0. The traditional starting point is (-1.2,1). The M-file banana.m defines the function.

function f = banana(x)
f = 100*(x(2)-x(1)^2)^2+(1-x(1))^2;

The statements

[x,out] = fmins('banana',[-1.2, 1]);
x
out(10)

produce

x =

    1.0000    1.0000

ans =

    165

This indicates that the minimizer was found to at least four decimal places in 165 steps.

Move the location of the minimum to the point [a,a^2] by adding a second parameter to banana.m.

function f = banana(x,a)
if nargin < 2, a = 1; end
f = 100*(x(2)-x(1)^2)^2+(a-x(1))^2;

Then the statement

[x,out] = fmins('banana', [-1.2, 1], [0, 1.e-8], [], sqrt(2));

sets the new parameter to sqrt(2) and seeks the minimum to an accuracy higher than the default.

Algorithm

The algorithm is the Nelder-Mead simplex search described in the two references. It is a direct search method that does not require gradients or other derivative information. If n is the length of x, a simplex in n-dimensional space is characterized by the n+1 distinct vectors which are its vertices. In two-space, a simplex is a triangle; in three-space, it is a pyramid.

At each step of the search, a new point in or near the current simplex is generated. The function value at the new point is compared with the function's values at the vertices of the simplex and, usually, one of the vertices is replaced by the new point, giving a new simplex. This step is repeated until the diameter of the simplex is less than the specified tolerance and the function values of the simplex vertices differ from the lowest function value by less than the specified tolerance, or the maximum number of function evaluations has been exceeded.