Jacobi elliptic functions
Syntax
[SN,CN,DN] = ellipj(U,M)
[SN,CN,DN] = ellipj(U,M,tol)
Definition
The Jacobi elliptic functions are defined in terms of the integral:
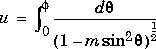
Then
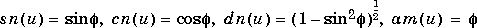
Some definitions of the elliptic functions use the modulus k instead of the parameter m. They are related by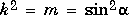 :
The Jacobi elliptic functions obey many mathematical identities; for a good sample, see [1].
:
The Jacobi elliptic functions obey many mathematical identities; for a good sample, see [1].
Description
[SN,CN,DN] = ellipj(U,M)
returns the Jacobi elliptic functions SN, CN, and DN, evaluated for corresponding elements of argument U and parameter M. Inputs U and M must be the same size (or either can be scalar).
[SN,CN,DN] = ellipj(U,M,tol)
computes the Jacobi elliptic functions to accuracy tol. The default is eps; increase this for a less accurate but more quickly computed answer.
Algorithm
ellipj computes the Jacobi elliptic functions using the method of the arithmetic-geometric mean [1]. It starts with the triplet of numbers:
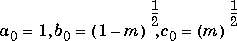
ellipj computes successive iterates with:
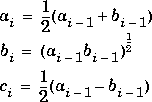
Next, it calculates the amplitudes in radians using:
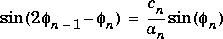
being careful to unwrap the phases correctly. The Jacobian elliptic functions are then simply:
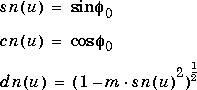
Limitations
The ellipj function is limited to the input domain 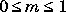 . Map other values of
. Map other values of M into this range using the transformations described in [1], equations 16.10 and 16.11. U is limited to real values.
See Also
ellipke Complete elliptic integrals of the first and second kind
References
[1] Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, 17.6.
[ Previous | Help Desk | Next ]
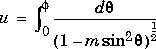
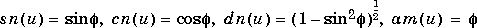
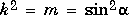 :
The Jacobi elliptic functions obey many mathematical identities; for a good sample, see [1].
:
The Jacobi elliptic functions obey many mathematical identities; for a good sample, see [1].
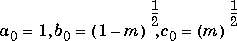
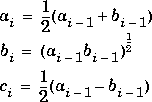
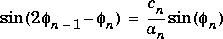
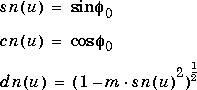
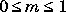 . Map other values of
. Map other values of