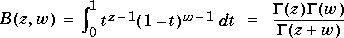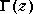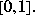Beta functions
Syntax
B = beta(Z,W)
I = betainc(X,Z,W)
L = betaln(Z,W)
Definition
The beta function is:
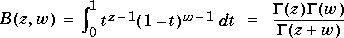
where 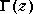
is the gamma function. The incomplete beta function is:

Description
B = beta(Z,W)
computes the beta function for corresponding elements of the complex arrays Z and W. The arrays must be the same size (or either can be scalar).
I = betainc(X,Z,W)
computes the incomplete beta function. The elements of X must be in the closed interval 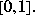
L = betaln(Z,W)
computes the natural logarithm of the beta function, log(beta(Z,W)), without computing beta(Z,W). Since the beta function can range over very large or very small values, its logarithm is sometimes more useful.
Examples
format rat
beta((0:10)',3)
ans =
1/0
1/3
1/12
1/30
1/60
1/105
1/168
1/252
1/360
1/495
1/660
In this case, with integer arguments,
beta(n,3)
= (n-1)!*2!/(n+2)!
= 2/(n*(n+1)*(n+2))
is the ratio of fairly small integers and the rational format is able to recover the exact result.
For x = 510, betaln(x,x) = -708.8616, which, on a computer with IEEE arithmetic, is slightly less than log(realmin). Here beta(x,x) would underflow (or be denormal).
Algorithm
beta(z,w) = exp(gammaln(z)+gammaln(w)-gammaln(z+w))
betaln(z,w) = gammaln(z)+gammaln(w)-gammaln(z+w)
[ Previous | Help Desk | Next ]