taylor (Symbolic Math Toolbox)

Symbolic Math Toolbox	Go to function:	Search Help Desk
taylor	Examples	See Also

Taylor series expansion.

Syntax

r = taylor(f)
r = taylor(f,n,v)
r = taylor(f,n,v,a)

Description

taylor(f,n,v) returns the (n-1)-order Maclaurin polynomial approximation to f, where f is a symbolic expression representing a function and v specifies the independent variable in the expression. v can be a string or symbolic variable.

taylor(f,n,v,a) returns the Taylor series approximation to f about a. The argument a can be a numeric value, a symbol, or a string representing a numeric value or an unknown.

You can supply the arguments n, v, and a in any order. taylor determines the purpose of the arguments from their position and type.

You can also omit any of the arguments n, v, and a. If you do not specify v, taylor uses findsym to determine the function's independent variable. n defaults to 6.

The Taylor series for an analytic function f(x) about the basepoint x=a is given below.

Examples

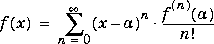
This table describes the various uses of the taylor command and its relation to Taylor and MacLaurin series.


Mathematical Operation	MATLAB
	`syms x` `taylor(f)`
, m is a positive integer	`taylor(f,m)` m is a positive integer
, a is a real number	`taylor(f,a)` a is a real number
m₁, m₂ are positive integers	`taylor(f,m1,m2)` `m₁, m₂ are positive integers`
a is real and m is a positive integer	`taylor(f,m,a)` `a is real and m is a positive integer`

In the case where f is a function of two or more variables (f=f(x,y,...)), there is a fourth parameter that allows you to select the variable for the Taylor expansion. Look at this table for illustrations of this feature.


Mathematical Operation	MATLAB
	`taylor(f,y)`
m is a positive integer	`taylor(f,y,m)` or `taylor(f,m,y)` m is a positive integer
a is real and m is a positive integer	`taylor(f,m,y,a)` a is real and m is a positive integer
a is real	`taylor(f,y,a)` a is real