MFUN Special Functions
Function Name |
Definition |
mfun Name |
Arguments |
Bernoulli Numbers and Polynomials |
Generating functions:
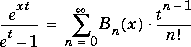
|
bernoulli(n)
bernoulli(n,t)
|
n 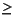 0
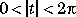
|
Bessel Functions |
BesselI, BesselJ - Bessel functions of the first kind.
BesselK, BesselY - Bessel functions of the second kind.
|
BesselJ(v,x)
BesselY(v,x)
BesselI(v,x)
BesselK(v,x)
|
v is real.
|
Beta Function |
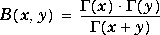
|
Beta(x,y)
|
|
Binomial Coefficients |
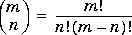

|
binomial(m,n)
|
|
Complete Elliptic Integrals |
Legendre's complete elliptic integrals of the first, second, and third kind. |
LegendreKc(k)
LegendreEc(k)
LegendrePic(a,k)
|
a is real
-Inf < a < Inf
k is real
0 < k < 1
|
Complete Elliptic Integrals with Complementary Modulus |
Associated complete elliptic integrals of the first, second, and third kind using complementary modulus. |
LegendreKc1(k)LegendreEc1(k)
LegendrePic1(a,k)
|
a is real
-Inf < a < Inf
k is real
0 < k < 1
|
Complementary Error Function and Its Iterated Integrals |

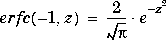

|
erfc(z)
erfc(n,z)
|
n > 0
|
Dawson's Integral |

|
dawson(x)
|
|
Digamma Function |

|
Psi(x)
|
|
Dilogarithm Integral |
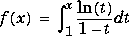
|
dilog(x)
|
x > 1
|
Error Function |
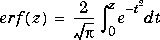
|
erf(z)
|
|
Euler Numbers and Polynomials |
Generating function for Euler numbers:
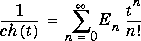
|
euler(n)euler(n,z)
|

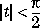
|
Exponential Integrals |
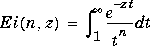
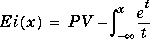
|
Ei(n,z)
Ei(x)
|
n 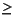 0
Real(z) > 0
|
Fresnel Sine and Cosine Integrals |
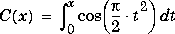
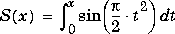
|
FresnelC(x)
FresnelS(x)
|
|
Gamma Function |

|
GAMMA(z)
|
|
Harmonic Function |
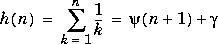
|
harmonic(n)
|
n > 0
|
Hyperbolic Sine and Cosine Integrals |
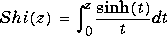

|
Shi(z)
Chi(z)
|
|
(Generalized) Hypergeometric Function |

where j and m are the number of terms in n and d, respectively.
|
hypergeom(n,d,x)
where n = [n1,n2,...]
d = [d1,d2,...]
|
n1,n2,... are real.
d1,d2,... are real and non-negative.
|
Incomplete Elliptic Integrals |
Legendre's incomplete elliptic integrals of the first, second, and third kind. |
LegendreF(x,k)
LegendreE(x,k)
LegendrePi(x,a,k)
|
0 < x  Inf
a is real
-Inf < a < Inf
k is real
0 < k < 1
|
Incomplete Gamma Function |
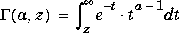
|
GAMMA(z1,z2)
|
|
Logarithm of the Gamma Function |
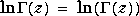
|
lnGAMMA(z)
|
|
Logarithmic Integral |
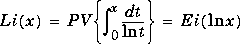
|
Li(x)
|
x > 1
|
Polygamma Function |
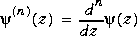
where 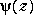 is the Digamma function.
is the Digamma function.
|
Psi(n,z)
|
n 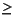 0
|
Shifted Sine Integral |

|
Ssi(z)
|
|
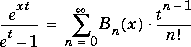
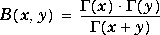
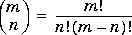


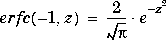



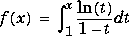
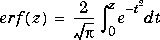
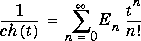
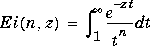
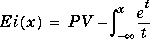
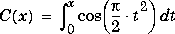
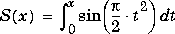

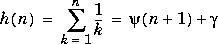
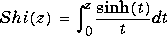



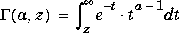
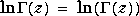
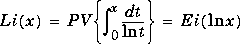
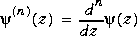

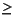
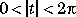

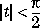
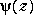 is the Digamma function.
is the Digamma function.