trapz (MATLAB Function Reference)

Trapezoidal numerical integration

Z = trapz(Y)
Z = trapz(X,Y)
Z = trapz(...,dim)

Description

Z = trapz(Y)

computes an approximation of the integral of Y via the trapezoidal method (with unit spacing). To compute the integral for spacing other than one, multiply Z by the spacing increment.

If Y is a vector, trapz(Y) is the integral of Y.

If Y is a matrix,trapz(Y) is a row vector with the integral over each column.

If Y is a multidimensional array, trapz(Y) works across the first nonsingleton dimension.

Z = trapz(X,Y)

computes the integral of Y with respect to X using trapezoidal integration.

If X is a column vector and Y an array whose first nonsingleton dimension is length(X), trapz(X,Y) operates across this dimension.

Z = trapz(...,dim)

integrates across the dimension of Y specified by scalar dim. The length of X, if given, must be the same as size(Y,dim).

Examples

The exact value of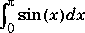

is 2.

To approximate this numerically on a uniformly spaced grid, use

X = 0:pi/100:pi;
Y = sin(x);

Then both

Z = trapz(X,Y)

and

Z = pi/100*trapz(Y)

produce

Z =
    1.9998

A nonuniformly spaced example is generated by

X = sort(rand(1,101)*pi);
Y = sin(X);
Z = trapz(X,Y);

The result is not as accurate as the uniformly spaced grid. One random sample produced

Z =
    1.9984