| MATLAB Function Reference | Search Help Desk |
| sprandsym | See Also |
Sparse symmetric random matrix
R = sprandsym(S) R = sprandsym(n,density) R = sprandsym(n,density,rc) R = sprandsym(n,density,rc,kind)
R = sprandsym(S)
returns a symmetric random matrix whose lower triangle and diagonal have the same structure as S. Its elements are normally distributed, with mean 0 and variance 1.
R = sprandsym(n,density)
returns a symmetric random, n-by-n, sparse matrix with approximately density*n*n nonzeros; each entry is the sum of one or more normally distributed random samples, and (0 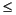
density 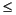
1).
R = sprandsym(n,density,rc)
returns a matrix with a reciprocal condition number equal to rc. The distribution of entries is nonuniform; it is roughly symmetric about 0; all are in  .
If
.
If rc is a vector of length n, then R has eigenvalues rc. Thus, if rc is a positive (nonnegative) vector then R is a positive definite matrix. In either case, R is generated by random Jacobi rotations applied to a diagonal matrix with the given eigenvalues or condition number. It has a great deal of topological and algebraic structure.
R = sprandsym(n,density,rc,kind)
returns a positive definite matrix. Argument kind can be:
1 to generate R by random Jacobi rotation of a positive definite diagonal matrix. R has the desired condition number exactly.
2 to generate an R that is a shifted sum of outer products. R has the desired condition number only approximately, but has less structure.
3 to generate an R that has the same structure as the matrix S and approximate condition number 1/rc. density is ignored.
sprand Sparse uniformly distributed random matrix
sprandn Sparse normally distributed random matrix