polyvalm (MATLAB Function Reference)

Matrix polynomial evaluation

Y = polyvalm(p,X)

Description

Y = polyvalm(p,X)

evaluates a polynomial in a matrix sense. This is the same as substituting matrix X in the polynomial p.

Polynomial p is a vector whose elements are the coefficients of a polynomial in descending powers, and X must be a square matrix.

Examples

The Pascal matrices are formed from Pascal's triangle of binomial coefficients. Here is the Pascal matrix of order 4.

X = pascal(4)
X =
    1    1    1    1
    1    2    3    4
    1    3    6   10
    1    4   10   20

Its characteristic polynomial can be generated with the poly function.

 p = poly(X)
 p = 
    1    -29    72    -29    1

This represents the polynomial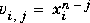

Pascal matrices have the curious property that the vector of coefficients of the characteristic polynomial is palindromic; it is the same forward and backward.

Evaluating this polynomial at each element is not very interesting.

 polyval(p,X) 
 ans =
    16      16      16      16
    16      15    -140    -563
    16    -140   -2549  -12089
    16    -563  -12089  -43779

But evaluating it in a matrix sense is interesting.

 polyvalm(p,X) 
 ans =
    0    0    0    0
    0    0    0    0
    0    0    0    0
    0    0    0    0

The result is the zero matrix. This is an instance of the Cayley-Hamilton theorem: a matrix satisfies its own characteristic equation.