pcg (MATLAB Function Reference)

pcg	Examples See Also

Preconditioned Conjugate Gradients method

Syntax

x = pcg(A,b)
pcg(A,b,tol)
pcg(A,b,tol,maxit)
pcg(A,b,tol,maxit,M)
pcg(A,b,tol,maxit,M1,M2)
pcg(A,b,tol,maxit,M1,M2,x0)
x = pcg(A,b,tol,maxit,M1,M2,x0)
[x,flag] = pcg(A,b,tol,maxit,M1,M2,x0) 
[x,flag,relres] = pcg(A,b,tol,maxit,M1,M2,x0)
[x,flag,relres,iter] = pcg(A,b,tol,maxit,M1,M2,x0)
[x,flag,relres,iter,resvec] = pcg(A,b,tol,maxit,M1,M2,x0)

Description

x = pcg(A,b)

attempts to solve the system of linear equations A*x = b for x. The coefficient matrix A must be symmetric and positive definite and the right hand side (column) vector b must have length n, where A is n-by-n. pcg will start iterating from an initial estimate that by default is an all zero vector of length n. Iterates are produced until the method either converges, fails, or has computed the maximum number of iterations. Convergence is achieved when an iterate x has relative residual norm(b-A*x)/norm(b) less than or equal to the tolerance of the method.The default tolerance is 1e-6. The default maximum number of iterations is the minimum of n and 20. No preconditioning is used.

pcg(A,b,tol)

specifies the tolerance of the method, tol.

pcg(A,b,tol,maxit)

additionally specifies the maximum number of iterations, maxit.

pcg(A,b,tol,maxit,M) and pcg(A,b,tol,maxit,M1,M2)

use left preconditioner M or M=M1*M2 and effectively solve the system inv(M)*A*x =inv(M)*b for x. If M1 or M2 is given as the empty matrix ([]), it is considered to be the identity matrix, equivalent to no preconditioning at all. Since systems of equations of the form M*y=r are solved using backslash within pcg, it is wise to factor preconditioners into their Cholesky factors first. For example, replace pcg(A,b,tol,maxit,M) with:

R = chol(M); 
pcg(A,b,tol,maxit,R',R).

The preconditioner M must be symmetric and positive definite.

pcg(A,b,tol,maxit,M1,M2,x0)

specifies the initial estimate x0. If x0 is given as the empty matrix ([]), the default all zero vector is used.

x = pcg(A,b,tol,maxit,M1,M2,x0)

returns a solution x. If pcg converged, a message to that effect is displayed. If pcg failed to converge after the maximum number of iterations or halted for any reason, a warning message is printed displaying the relative residual norm(b-A*x)/norm(b) and the iteration number at which the method stopped or failed.

[x,flag] = pcg(A,b,tol,maxit,M1,M2,x0)

returns a solution x and a flag which describes the convergence of pcg:


Flag	Convergence
`0`	`pcg` converged to the desired tolerance `tol` within `maxit` iterations without failing for any reason.
`1`	`pcg` iterated `maxit` times but did not converge.
`2`	One of the systems of equations of the form `M*y = r` involving the preconditioner was ill-conditioned and did not return a useable result when solved by `\` (backslash).
`3`	The method stagnated. (Two consecutive iterates were the same.)
`4`	One of the scalar quantities calculated during `pcg` became too small or too large to continue computing

Whenever flag is not 0, the solution x returned is that with minimal norm residual computed over all the iterations. No messages are displayed if the flag output is specified.

[x,flag,relres] = pcg(A,b,tol,maxit,M1,M2,x0)

also returns the relative residual norm(b-A*x)/norm(b). If flag is 0, then relres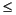

tol.

[x,flag,relres,iter] = pcg(A,b,tol,maxit,M1,M2,x0)

also returns the iteration number at which x was computed. This always satisfies 0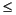

iter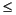

maxit.

[x,flag,relres,iter,resvec] = pcg(A,b,tol,maxit,M1,M2,x0)

also returns a vector of the residual norms at each iteration, starting from
resvec(1) = norm(b-A*x0). If flag is 0, resvec is of length iter+1 and resvec(end)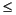

tol*norm(b).

Examples

A = delsq(numgrid('C',25))
b = ones(length(A),1)
[x,flag] = pcg(A,b)

flag is 1 since pcg will not converge to the default tolerance of 1e-6 within the default 20 iterations.

R = cholinc(A,1e-3)
[x2,flag2,relres2,iter2,resvec2] = pcg(A,b,1e-8,10,R',R)

flag2 is 0 since pcg will converge to the tolerance of 1.2e-9 (the value of relres2) at the sixth iteration (the value of iter2) when preconditioned by the incomplete Cholesky factorization with a drop tolerance of 1e-3. resvec2(1) = norm(b) and resvec2(7) = norm(b-A*x2).You may follow the progress of pcg by plotting the relative residuals at each iteration starting from the initial estimate (iterate number 0) with semilogy(0:iter2,resvec2/norm(b),'-o').