Associated Legendre functions
Syntax
P = legendre(n,X)
S = legendre(n,X,'sch')
Definition
The Legendre functions are defined by:
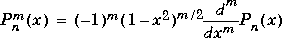
where 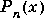
is the Legendre polynomial of degree n:
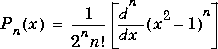 The Schmidt seminormalized associated Legendre functions are related to the nonnormalized associated Legendre functions
The Schmidt seminormalized associated Legendre functions are related to the nonnormalized associated Legendre functions 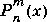
by:
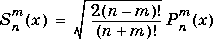
Description
P = legendre(n,X)
computes the associated Legendre functions of degree n and order m = 0,1,...,n, evaluated at X. Argument n must be a scalar integer less than 256, and X must contain real values in the domain 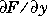 The returned array
The returned array P has one more dimension than X, and each element P(m+1,d1,d2...) contains the associated Legendre function of degree n and order m evaluated at X(d1,d2...).
If X is a vector, then P is a matrix of the form:
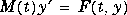
S = legendre(...,'sch')
computes the Schmidt seminormalized associated Legendre functions 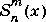 .
.
Examples
The statement legendre(2,0:0.1:0.2) returns the matrix:
|
x = 0
|
x = 0.1
|
x = 0.2
|
m = 0
|
0.5000
|
0.4850
|
0.4400
|
m = 1
|
0
|
0.2985
|
0.5879
|
m = 2
|
3.0000
|
2.9700
|
2.8800
|
Note that this matrix is of the form shown at the bottom of the previous page.
Given,
X = rand(2,4,5); N = 2;
P = legendre(N,X)
Then size(P) is 3-by-2-by-4-by-5, and P(:,1,2,3) is the same as legendre(n,X(1,2,3)).
[ Previous | Help Desk | Next ]
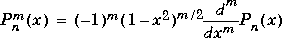
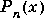
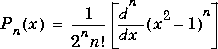 The Schmidt seminormalized associated Legendre functions are related to the nonnormalized associated Legendre functions
The Schmidt seminormalized associated Legendre functions are related to the nonnormalized associated Legendre functions 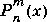
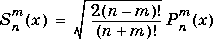
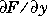 The returned array
The returned array 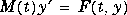
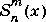 .
The statement
.
The statement