Kronecker tensor product
Syntax
K = kron(X,Y)
Description
K = kron(X,Y)
returns the Kronecker tensor product of X and Y. The result is a large array formed by taking all possible products between the elements of X and those of Y. If X is m-by-n and Y is p-by-q, then kron(X,Y) is m*p-by-n*q.
Examples
If X is 2-by-3, then kron(X,Y) is
[ X(1,1)*Y X(1,2)*Y X(1,3)*Y
X(2,1)*Y X(2,2)*Y X(2,3)*Y ]
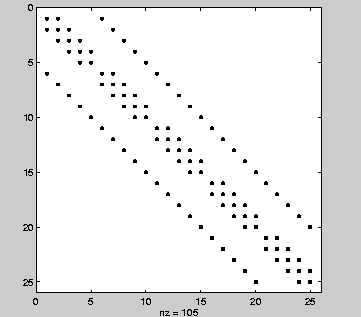
The matrix representation of the discrete Laplacian operator on a two-dimensional, n-by-n grid is a n^2-by-n^2 sparse matrix. There are at most five nonzero elements in each row or column. The matrix can be generated as the Kronecker product of one-dimensional difference operators with these statements:
I = speye(n,n);
E = sparse(2:n,1:n-1,1,n,n);
D = E+E'-2*I;
A = kron(D,I)+kron(I,D);
Plotting this with the spy function for n = 5 yields:
[ Previous | Help Desk | Next ]
