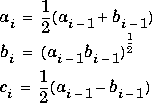Exponential integral
Syntax
Y = expint(X)
Definitions
The exponential integral is defined as:
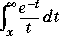
Another common definition of the exponential integral function is the Cauchy principal value integral:
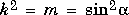
which, for real positive x, is related to expint as follows:
expint(-x+i*0) = -Ei(x) - i*pi
Ei(x) = real(-expint(-x))
Description
Y = expint(X)
evaluates the exponential integral for each element of X.
Algorithm
For elements of X in the domain 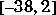
, expint uses a series expansion representation (equation 5.1.11 in [1]):
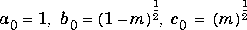 For all other elements of
For all other elements of X, expint uses a continued fraction representation (equation 5.1.22 in [1]):
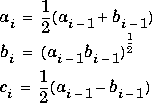
References
[1] Abramowitz, M. and I. A. Stegun. Handbook of Mathematical Functions. Chapter 5, New York: Dover Publications, 1965.
[ Previous | Help Desk | Next ]
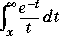
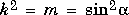
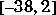
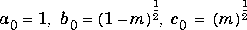 For all other elements of
For all other elements of