| MATLAB Function Reference | Search Help Desk |
| colmmd | Examples See Also |
Sparse column minimum degree permutation
p = colmmd(S)
p = colmmd(S)
returns the column minimum degree permutation vector for the sparse matrix S. For a nonsymmetric matrix S, this is a column permutation p such that S(:,p) tends to have sparser LU factors than S.
The colmmd permutation is automatically used by \ and / for the solution of nonsymmetric and symmetric indefinite sparse linear systems.
Use spparms to change some options and parameters associated with heuristics in the algorithm.
The minimum degree algorithm for symmetric matrices is described in the review paper by George and Liu [1]. For nonsymmetric matrices, MATLAB's minimum degree algorithm is new and is described in the paper by Gilbert, Moler, and Schreiber [2]. It is roughly like symmetric minimum degree for A'*A, but does not actually form A'*A.
Each stage of the algorithm chooses a vertex in the graph of A'*A of lowest degree (that is, a column of A having nonzero elements in common with the fewest other columns), eliminates that vertex, and updates the remainder of the graph by adding fill (that is, merging rows). If the input matrix S is of size m-by-n, the columns are all eliminated and the permutation is complete after n stages. To speed up the process, several heuristics are used to carry out multiple stages simultaneously.
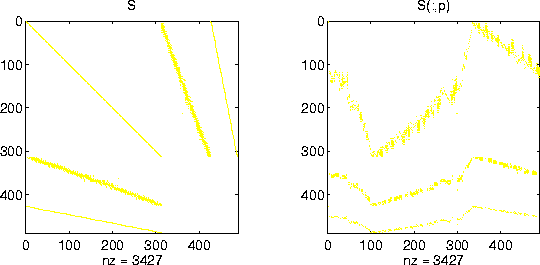
The Harwell-Boeing collection of sparse matrices includes a test matrix ABB313. It is a rectangular matrix, of order 313-by-176, associated with least squares adjustments of geodesic data in the Sudan. Since this is a least squares problem, form the augmented matrix (see spaugment), which is square and of order 489. The spy plot shows that the nonzeros in the original matrix are concentrated in two stripes, which are reflected and supplemented with a scaled identity in the augmented matrix. The colmmd ordering scrambles this structure. (Note that this example requires the Harwell-Boeing collection of software.)
load('abb313.mat')
S = spaugment(A);
p = colmmd(S);
spy(S)
spy(S(:,p))

Comparing the spy plot of the LU factorization of the original matrix with that of the reordered matrix shows that minimum degree reduces the time and storage requirements by better than a factor of 2.6. The nonzero counts are 18813 and 7223, respectively.
spy(lu(S)) spy(lu(S(:,p)))
\ Backslash or matrix left division
colperm Sparse column permutation based on nonzero count
lu LU matrix factorization
spparms Set parameters for sparse matrix routines
symmmd Sparse symmetric minimum degree ordering
symrcm Sparse reverse Cuthill-McKee ordering