| Getting Started with MATLAB | Search Help Desk |
More About Matrices and Arrays
This sections shows you more about working with matrices and arrays, focusing onA =
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
provides several examples that give a taste of MATLAB matrix operations. You've already seen the matrix transpose, A'. Adding a matrix to its transpose produces a symmetric matrix.
A + A'
ans =
32 8 11 17
8 20 17 23
11 17 14 26
17 23 26 2
The multiplication symbol, *, denotes the matrix multiplication involving inner products between rows and columns. Multiplying a matrix by its transpose also produces a symmetric matrix.
A'*A ans = 378 212 206 360 212 370 368 206 206 368 370 212 360 206 212 378The determinant of this particular matrix happens to be zero, indicating that the matrix is singular.
d = det(A)
d =
0
The reduced row echelon form of A is not the identity.
R = rref(A)
R =
1 0 0 1
0 1 0 -3
0 0 1 3
0 0 0 0
Since the matrix is singular, it does not have an inverse. If you try to compute the inverse with
X = inv(A)you will get a warning message
Warning: Matrix is close to singular or badly scaled.
Results may be inaccurate. RCOND = 1.175530e-017.
Roundoff error has prevented the matrix inversion algorithm from detecting exact singularity. But the value of rcond, which stands for reciprocal condition estimate, is on the order of eps, the floating-point relative precision, so the computed inverse is unlikely to be of much use.
The eigenvalues of the magic square are interesting.
e = eig(A)
e =
34.0000
8.0000
0.0000
-8.0000
One of the eigenvalues is zero, which is another consequence of singularity. The largest eigenvalue is 34, the magic sum. That's because the vector of all ones is an eigenvector.
v = ones(4,1)
v =
1
1
1
1
A*v
ans =
34
34
34
34
When a magic square is scaled by its magic sum,
P = A/34the result is a doubly stochastic matrix whose row and column sums are all one.
P =
0.4706 0.0882 0.0588 0.3824
0.1471 0.2941 0.3235 0.2353
0.2647 0.1765 0.2059 0.3529
0.1176 0.4412 0.4118 0.0294
Such matrices represent the transition probabilities in a Markov process. Repeated powers of the matrix represent repeated steps of the process. For our example, the fifth power
P^5is
0.2507 0.2495 0.2494 0.2504
0.2497 0.2501 0.2502 0.2500
0.2500 0.2498 0.2499 0.2503
0.2496 0.2506 0.2505 0.2493
This shows that as k approaches infinity, all the elements in the kth power, Pk, approach 1/4.
Finally, the coefficients in the characteristic polynomial
poly(A)are
1 -34 -64 2176 0This indicates that the characteristic polynomial det( A -
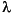I )
is
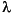4 - 34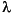3 - 64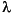2 + 2176
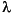The constant term is zero, because the matrix is singular, and the coefficient of the cubic term is -34, because the matrix is magic!
When they are taken away from the world of linear algebra, matrices become two dimensional numeric arrays. Arithmetic operations on arrays are done element-by-element. This means that addition and subtraction are the same for arrays and matrices, but that multiplicative operations are different. MATLAB uses a dot, or decimal point, as part of the notation for multiplicative array operations.
The list of operators includes:
A.*Athe result is an array containing the squares of the integers from 1 to 16, in an unusual order.
ans =
256 9 4 169
25 100 121 64
81 36 49 144
16 225 196 1
Array operations are useful for building tables. Suppose n is the column vector
n = (0:9)';Then
pows = [n n.^2 2.^n]builds a table of squares and powers of two.
pows =
0 0 1
1 1 2
2 4 4
3 9 8
4 16 16
5 25 32
6 36 64
7 49 128
8 64 256
9 81 512
The elementary math functions operate on arrays element by element. So
format short g x = (1:0.1:2)'; logs = [x log10(x)]builds a table of logarithms.
logs =
1.0 0
1.1 0.04139
1.2 0.07918
1.3 0.11394
1.4 0.14613
1.5 0.17609
1.6 0.20412
1.7 0.23045
1.8 0.25527
1.9 0.27875
2.0 0.30103
MATLAB uses column-oriented analysis for multivariate statistical data. Each column in a data set represents a variable and each row an observation. The (i,j)th element is the ith observation of the jth variable.
As an example, consider a data set with three variables:
D =
72 134 3.2
81 201 3.5
69 156 7.1
82 148 2.4
75 170 1.2
The first row contains the heart rate, weight, and exercise hours for patient 1, the second row contains the data for patient 2, and so on. Now you can apply many of MATLAB's data analysis functions to this data set. For example, to obtain the mean and standard deviation of each column:
mu = mean(D), sigma = std(D) mu = 75.8 161.8 3.48 sigma = 5.6303 25.499 2.2107For a list of the data analysis functions available in MATLAB, type
help datafunIf you have access to the Statistics Toolbox, type
help statsMatrices and scalars can be combined in several different ways. For example, a scalar is subtracted from a matrix by subtracting it from each element. The average value of the elements in our magic square is 8.5, so
B = A - 8.5forms a matrix whose column sums are zero.
B =
7.5 -5.5 -6.5 4.5
-3.5 1.5 2.5 -0.5
0.5 -2.5 -1.5 3.5
-4.5 6.5 5.5 -7.5
sum(B)
ans =
0 0 0 0
With scalar expansion, MATLAB assigns a specified scalar to all indices in a range. For example:
B(1:2,2:3) = 0zeros out a portion of
B
B =
7.5 0 0 4.5
-3.5 0 0 -0.5
0.5 -2.5 -1.5 3.5
-4.5 6.5 5.5 -7.5
The logical vectors created from logical and relational operations can be used to reference subarrays. Suppose X is an ordinary matrix and L is a matrix of the same size that is the result of some logical operation. Then X(L) specifies the elements of X where the elements of L are nonzero.
This kind of subscripting can be done in one step by specifying the logical operation as the subscripting expression. Suppose you have the following set of data.
x = 2.1 1.7 1.6 1.5 NaN 1.9 1.8 1.5 5.1 1.8 1.4 2.2 1.6 1.8The
NaN is a marker for a missing observation, such as a failure to respond to an item on a questionnaire. To remove the missing data with logical indexing, use finite(x), which is true for all finite numerical values and false for NaN and Inf.
x = x(finite(x)) x = 2.1 1.7 1.6 1.5 1.9 1.8 1.5 5.1 1.8 1.4 2.2 1.6 1.8Now there is one observation,
5.1, which seems to be very different from the others. It is an outlier. The following statement removes outliers, in this case those elements more than three standard deviations from the mean.
x = x(abs(x-mean(x)) <= 3*std(x)) x = 2.1 1.7 1.6 1.5 1.9 1.8 1.5 1.8 1.4 2.2 1.6 1.8For another example, highlight the location of the prime numbers in Dürer's magic square by using logical indexing and scalar expansion to set the nonprimes to 0.
A(~isprime(A)) = 0
A =
0 3 2 13
5 0 11 0
0 0 7 0
0 0 0 0
The find function determines the indices of array elements that meet a given logical condition. In its simplest form, find returns a column vector of indices. Transpose that vector to obtain a row vector of indices. For example
k = find(isprime(A))'picks out the locations, using one-dimensional indexing, of the primes in the magic square.
k =
2 5 9 10 11 13
Display those primes, as a row vector in the order determined by k, with
A(k)
ans =
5 3 2 11 7 13
When you use k as a left-hand-side index in an assignment statement, the matrix structure is preserved.
A(k) = NaN
A =
16 NaN NaN NaN
NaN 10 NaN 8
9 6 NaN 12
4 15 14 1