Math 110.211: Honors Multivariable Calculus
Spring
2008 Course Syllabus
http://www.mathematics.jhu.edu/brown/Spring08211.htm
|
MW 12:00pm - 1:15pm: Room Shaffer 304 |
|||
|
. |
|||
|
403 Krieger
Hall |
|
||
|
410-516-8179 |
|
||
|
Office
Hours: |
M |
2:30-3:30 pm |
by appt. other times |
|
W |
2:30-3:30 pm |
||
|
Below is some basic information relevant to this course.� A more detailed schedule of course material, homework assignments, and testing dates will follow shortly. |
Text:� Vector Calculus, 3rd Edition by Susan Jane Colley ,ISBN-10: 0131858742
Current Recitation Sections:
|
Section |
Time |
Place |
Instructor |
|
1 |
Friday 12:00pm |
Shaffer 304 |
Course Material: The core of the course will center on the text material, and will cover the portions of the book detailed below.
Grade Policy:��� There will be homework sets offered weekly (30%), 2 in-lecture exams (40%) and a final (30%).� The schedule of these exams is given with the homework problems below.� There will be no make-ups on homework or exams.� If you miss an exam, you will have to be cleared by the department to be excused from the exam.� This only means, however, that the ultimate grade for that exam will be calculated based on your performance on future exams and the final.�
Homework: �� Homework
based on the week�s lectures will be posted on the course web site sometime on
Tuesday. That assignment will be due the following Wednesday
at the start of lecture. You are encouraged to do your homework in
groups. You are required, however, to write up your homework on your own.
Homework is essential educational part of the course. You will be graded mostly
on your ability to work problems on quizzes and exams. You cannot work problems
on quizzes and exams if you have not practiced the techniques within the
homework problems. If you misuse homework by not doing it yourself, or not
checking that you can solve a problem on your own after having been shown how
to do it, then your exam scores and corresponding grade will reflect this. Talk
to Patrick Zulkowski about how
to turn in a homework if you cannot go to class.
Course Policy: You are
responsible for lecture notes, any course material handed out, and attendance
in class.� While I will not formally
record your attendance, I will get to know you and your rate of presence over time.� The quizzes are designed to evaluate your
understanding of the current focus of the class.� They will strongly mimic homework
assignment problems.� The
lectures will be conducted as if you have already read the material and
attempted some homework problems. �In this manner, you can focus mainly on those
parts of the lectures that cover the areas of your reading you found difficult
to understand. My teaching style is that of interactive discussion and I will
rely on your input in developing the material.�
Active participation in the classroom is a great way to generate the
discussion necessary to fully grasp the material.
Help Room: ���� 213 Kreiger Hall.� The hours are 9am � 9pm on Monday through Thursday, and 9am � 5pm on Friday.� This free service is a very valuable way to get one-on-one help on the current material of a class from other students outside the course.� It is staffed by graduate students and advanced undergraduates.
Ethics Statement: The strength
of the university depends on academic and personal integrity. In this course,
you must be honest and truthful. Ethical violations
include cheating on exams, plagiarism, reuse of assignments, improper use of the Internet and electronic devices,
unauthorized collaboration, alteration of graded
assignments, forgery and falsification, lying,
facilitating academic dishonesty, and unfair competition.
Report
any violations you witness to the instructor. You may consult the associate dean of students
and/or the chairman of the Ethics Board beforehand.
See the guide on "Academic Ethics for Undergraduates" and the Ethics Board web site http://ethics.jhu.edu
for more information.
Students with Disabilities: Students
with documented disabilities or other special needs that require accommodation must
register with the Office of Academic Advising. After that, remind me of your
needs at least 5 days prior to each exam; we will need to have received
confirmation from Academic Advising.
Spring
2008 Tentative Schedule
The details of this material
will be updated and reformed as the semester progresses.
|
Week |
Sections |
Homework |
Due in Lecture |
|
January 28, 30 |
Course Overview |
|
February 6 |
|
1.1 Vectors 1.2 More About Vectors 1.3 The Dot Product 1.4 The Cross Product 1.5 Equations for Planes |
22,25 |
||
|
February 4, 6 |
1.7 New Coordinate Systems 1.8 Chapter 1 Extra 2.1 Functions of Several Variables |
2, 4, 8, 10, 16, 18 Verify and/or explain: 12,18,22,26,EP1,EP2 2,4,9,15,32,34,36,47 |
February 13 |
|
February 11, 13 |
2.2 Limits 2.3 Derivatives |
3,6,8,18,22,30,42,44,46,48,EP3 5,10 |
February 20 |
|
February 18, 20 |
2.3 Derivatives 2.4 Properties of Derivatives ������ (no 2.5 Chain Rule |
18,21,28,30,36,50 6,11,20,21 2,6,10 |
February 27 |
|
February 25, 27 |
2.5 Chain Rule 2.6 Directional Derivative/Gradient ����� (Implicit/Inverse Fnc Thms) 3.1 Parameterized Curves (no Kepler) |
12,16,23,28,29 4,12,17,22,34,40,46 (see here for a discussion of the Imp. Fnc Thm) 4,9,18,26,30 |
March 5 |
|
March 3 |
3.2 Arc Length (no geometry) 3.3 Vector Fields |
3,4,18,20 |
March 12 |
|
March 5 |
Exam 1 |
All listed sections up to February 27 |
|
|
March
10 |
Canceled |
|
|
|
March
12 |
3.3 Vector Fields 3.4 Div, Grad, Curl. 3.5 Chapter 3 Extra 4.1 Differentials/Taylor�s Thm. |
26,30,31 28,31,32,EP5 Verify and/or explain: 1,2,3,19,24,29,30 4,15,18,26 |
March 26 |
|
March 17, 19 |
Spring Break |
||
|
March 24, 26 |
4.2 Extrema of Functions 4.3 Lagrange Multipliers |
2,22,32,35,46 17,18,24,26 |
April 2 |
|
March 31, April 2 |
5.1 Areas and Volumes 5.2 Double Integrals 5.3 Changing Order of Integration 5.4 Triple Integrals |
16 6,13,20,25,28,EP6 1,10,14 9 |
April 9 |
|
April 7, 9 |
5.5 Change of Variables 6.1 Line Integrals 6.2 Green�s Theorem |
6,7,8,23 10,18,23,28,EP7 6,19,20,23 |
April 16 |
|
April 14, 16 |
7.1 Parameterized Surfaces 7.2 Surface Integrals 7.5 T/F Exercises |
1,4,6,18,28 3,9,12,14,24,25 Verify and/or disprove: 14,20,22 |
April 23 |
|
April 21, 23 |
7.3 Stoke�s and Gauss� Theorems 7.5 T/F Exercises 8.1 Differential Forms |
4,8,16,17,18,19,21 Verify and/or disprove: 24,30 |
April 30 |
|
April 28 |
Exam 2 |
All included sections from 3.2 to 7.3 |
|
|
April 30 |
Generalized Stoke�s Thm and the FTC |
See here for an example calculation, |
|
|
May 5-7 |
Reading Period |
||
|
|
|
|
|
|
May 12 |
Final Exam Number 7 Solution |
9am - 12pm Room:
Krieger 300 New Room! |
|
Extra
Problems (labeled by EP# in homework):� Let 
�denote the real n-dimensional space where n
is a natural number, and 
.� For 
, we denote 
.
EP1: Do the following:
a.
Show the function 
is injective if at least one of its component functions is
injective.
b.
Show 
is surjective if all of its components are surjective.
EP2: Let
and 
be two vectors in 
which are not on the same line, so that the equation 
defines
a plane parameterized by the two real variables s, t.� Given the non-parameterized equation of the plane 
, write the constants A,
B, C, D in terms of , and 
.
EP3: Let
be open.� Show 
is continuous at 
�iff 
.
EP4: Show
that the length of a differentiable curve in 
is independent of its parameterization (Hint:� Use the Chain Rule).
EP5: Modify the proof of formula (4) of Theorem 4.5, page 219, to verify formula (3).�
EP6: Let
be continuous on the rectangular region 
.� For 
and 
, define 
.� Show that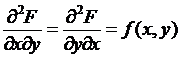 
.� This says that Fubini�s
Theorem for continuous functions implies the equality of mixed partials.
EP7: Let
be a gradient vector field on a domain which contains a curve 
.� Show that 
.� Discuss what one can
say in general about line integrals of gradient vector fields over curves, in
terms of the actual path one takes from any chosen point A to another point
B?� What about if the curve is closed?