Math 110.421, Dynamical Systems

Spring 2010 Course Syllabus

http://www.mathematics.jhu.edu/brown/courses/s10/Spring10421.htm

 

 

 

 

Text:  B. Hasselblat and A. Katok, A First Course in Dynamics, 1^st edition, Cambridge University Press (2003), ISBN 0 521 58750 6 (paperback).

 

Course Material: The core of the course will center on the text material, and will cover most of the book.

 

Grade Policy:    There will be homework sets and a (possibly take home) exam or two.  The schedule of homework and the exams will be given below in time. 

 

Homework:    Homework based on the current week’s lectures will be posted here on the course web site sometime on Thursday after lecture. These assignments will be due the following Thursday. You are strongly encouraged to do your homework in groups. You are required, however, to write up your homework on your own. Homework is essential educational part of this course. You will be graded mostly on your ability to work through problems completely and concisely.  This effort will be evaluated on the exam, which cannot be done in any collaborative way.

 

Course Policy: You are responsible for lecture notes, any course material handed out, and attendance in class.  While I will not formally record your attendance, I will easily get to know you and your rate of presence over time.  Since I will be following the book, the lectures will be conducted as if you have already read the material and attempted some homework problems.  In this manner, you can focus mainly on those parts of the lectures that cover the areas of your reading you found difficult to understand. My teaching style is that of interactive discussion and I will rely on your input in developing the material.  Active participation in the classroom is a great way to generate the discussion necessary to fully grasp the material.

 

Help Room:      213 Kreiger Hall.  The hours are 9am  9pm on Monday through Thursday, and 9am  5pm on Friday.  This free service is a very valuable way to get one-on-one help on the current material of a class from other students outside the course.  It is staffed by graduate students and advanced undergraduates.

Ethics Statement:  The strength of the university depends on academic and personal integrity. In this course, you must be honest and truthful.  Cheating is wrong. Cheating hurts our community by undermining academic integrity, creating mistrust, and fostering unfair competition. The university will punish cheaters with failure on an assignment, failure in a course, permanent transcript notation, suspension, and/or expulsion. Offenses may be reported to medical, law, or other professional or graduate schools when a cheater applies.

Violations can include cheating on exams, plagiarism, reuse of assignments without permission, improper use of the Internet and electronic devices unauthorized collaboration, alteration of graded assignments, forgery and falsification, lying, facilitating academic dishonesty, and unfair competition. Ignorance of these rules is not an excuse.

In this course, as in many math courses, working in groups to study particular problems and discuss theory is strongly encouraged.  Your ability to talk mathematics is of particular importance to your general understanding of mathematics.

You should collaborate with other students in this course on the general construction of homework assignment problems.  However, you must write up the solutions to these homework problems individually and separately.  If there is any question as to what this statement means, please see the professor or the grader.

For more information, see the guide on "Academic Ethics for Undergraduates" and the Ethics Board web site (http://ethics.jhu.edu).

Students with Disabilities:  Students with documented disabilities or other special needs that require accommodation must register with the Office of Academic Advising. After that, remind me of your needs at least 5 days prior to each exam; we will need to have received confirmation from Academic Advising.

Math 110.421, Dynamical Systems

Spring 2010 Tentative Schedule

 

The details of this material may be updated and reformed as the semester progresses.

 

 

Problem Notes:

*a.          Use the ratio  to construct a map on the interval  which defines the dynamical system.  Interestingly, the fixed point of this map will be the asymptotic growth rate for the rabbit population.

*b.         You may want to review Proposition 2.6.7 on page 63, showing that the metric defined on the circle is actually a metric.

*c.          This is actually easier than you may think.  With , you know the value of .   Just get it close to an integer.

 

Extra Problems:

 

EP1:    Approximate  using Heron’s method for calculating square roots, to an accuracy of .001.  Try this using starting points of 10 and 11 for your rectangle sides, and 1 and 110, noting the convergence properties.

EP2:    Do the following for the ODE :

a)   Solve the ODE by separating variables.  Justify why the absolute value sign is not necessary when stating a single expression for the general solution.

b)    Calculate the equivalent discrete dynamical system (on the real line) which takes each point of the real line to its position along the solution curve of the ODE one time unit later.  (Hint:  As in class, the function which defines the discrete dynamical system will be linear, but this case will include a specific, non-zero constant term).

c)   Discuss the simple dynamics of the discrete dynamical system.      

EP3:    Show  is a  -contraction on  without using any derivative material (that is, without using Propositions 2.2.3 or 2.2.5).

EP4:    Show, without using the Contraction Principle, that a contraction cannot have 2 or more fixed points.

EP5:    Find all periodic points (to an accuracy of  ) of the discrete dynamical system given by the map  on .

EP6:    Show that an invertible map on , where , must satisfy all of the following (Hint:  All of these can be shown by assuming the property does not hold and then finding a contradiction). 

                                                                      i.     Be injective (one-to-one),

                                                                    ii.     Be surjective (onto; the range must be all of  ),

                                                                 iii.     And either  and  or  and .

EP7:    Figure 2.2.4 provides a visual example of an invertible map on the unit circle (called  ) that contains homoclinic points.  Construct an example (similar to the one in the figure or different) with an explicit expression for .  Note:  Any continuous map of the unit interval with both endpoints fixed can be viewed as a map on .  But can you construct one that doesn’t fix the endpoints?  Can you construct one that is also differentiable on all of ?

EP8:    Solve the first order, autonomous, non-linear ODE system given in cylindrical coordinates below and show that there exists an asymptotically stable limit cycle (Hint:  Since the system is completely uncoupled, you can solve each ODE separately).  What are the eigenvalues of the  -periodic point ?

 

EP9:    Show that the logistic map  on  does not induce a discrete dynamical system for .

EP10:  Show that for , there is an attracting fixed point at .

EP11:  Find the change in variables which takes  to .

EP12:  Show that the annulus  below (in gray with its boundary circles) is homeomorphic to the cylinder  of height  and radius  centered on the z-axis and resting on the  plane.  Of course,  has no top or bottom, but the sides do have the circle edges at the top and bottom.  Do this by constructing the map  and its inverse  .  Hint:  A good way to do this is to construct  from (part of) the plane into three-space using polar coordinates in the plane and cylindrical coordinates in three space.  Construct  in a similar manner.  When restricted to  and , the maps should be continuous bijections.  Verify this.

 

 

 

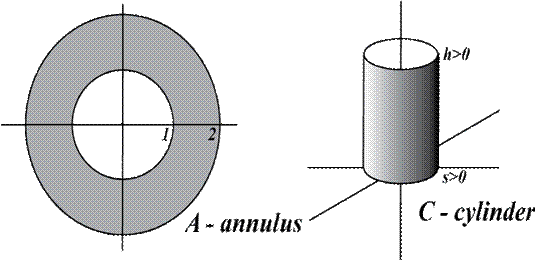
EP13:  Show that you cannot have a continuous surjective contraction on .  However, construct a continuous, non-trivial contraction on the circle. Hint:  A continuous map cannot break the circle in its image (it would not be continuous at the break), but it can fold the circle.

EP14:  Show that the function  from the plane to itself can be made into a function on the standard infinite cylinder .  Show also that by limiting the domain appropriately, one can use g to construct a function on the torus .

For the next two problems, let , where .

 

EP15:  If  (no absolute values here:  both eigenvalues are positive), find the 2-dimensional system of linear, homogeneous, first order ODEs whose time-1 map is .

EP16:  If  (I want absolute values here), the equation of the curves of motion where the solutions live are given by , where .  Derive this equation for the lines of motion.

 

EP17:  Do the following:

a)   For the hyperbolic map  given by , and , find a nontrivial initial vector  so that the orbit of  goes to the origin.  That is, . 

b)   Draw a phase portrait of  giving the invariant curves (use a range of -15 to 15 for the axes).  Show  for the  you found in part a) and for .

c)   Recast the Lemmings Problem as a first order vector recursion in the plane.  Find the starting vector.

d)   Use Proposition 3.1.13 to find the functional form for the yearly population of lemmings.  Use this to determine the total population of lemmings this spring, if the first two lemmings were one year old in 1980.

EP18:  Show the following:

a)   For any rational rotation of the circle, all orbits are periodic of the same period.

b)   For any irrational orbit, no orbits are periodic.

EP19:  In class, the circle rotation  was discussed, where

and .  It was determined that  was the closest return map to  than the previous iterates, and it was stated that it was smaller than .  Show this using the continued fraction form of .

EP20:  Show that a linear map on the real line of the form  corresponds to a continuous map on  iff  is an integer.  Graph the circle map  in the unit square by considering the function as a map on the unit interval with the endpoints identified.  Note:  Two points in the real line correspond to the same point on the circle if their difference is an integer.  

EP21:  In general, let ,   where  and  the integers. 

a)   Show  induces a map on the standard 2-torus .  Hint:  Two vectors in the plane are in the same equivalence class on the torus (correspond to the same point on the tours), if they differ by a vector with integer entries.

b)   What can you say about the orbits of points on  given by

                                                                      i.      

                                                                    ii.      

                                                                 iii.      

EP22:  In the proof of Proposition 4.2.8 on page 113 of the text, it is claimed that the first return map on the waist curve under the constant flow induced by  which is not rational, is a rotation by , .  Show this.

EP23:  Draw the Lissajous figure corresponding to the  -planar projection of the toral flow given in Section 4.2.4 when  and .  Now, for these same values of , draw the orbit of the origin on the torus using the unit square with the proper side identifications as the model (and not the actual “surface-of-a-donut” realization of the torus).

EP24:  Find the rotation number for the following invertible circle map:

 

EP25:  Show that for a circle map  with a lift  that the function  is periodic.

EP26:  Find a suitable lift  for the rotation map,  where .  Graph both  and .

EP27:  Do the following:

a)   Show that the constant flow on the standard 2-torus is an isometry (Hint: Build the proper metric on the torus.)

b)   Show that the map  on the unit cylinder  preserves volume (though it is not an isometry).

EP28:  For the normalized un-damped pendulum , carefully draw either the phase plane or the phase cylinder.  Re-derive the potential energy and the total energy of the system and show the total energy is a constant of the motion.  Label on your drawing the energy levels of the equilibria and describe what is happening on the orbits that comprise the energy level that includes the saddle.  Do the closed orbits in phase space all have the same period? Explain.

EP29:  For the circular billiard within the unit circle, derive the expression for the caustic as a function of the incidence angle for the light ray.

EP30:  Derive an expression for the twist map on the state space cylinder, which is the billiard map for the circular table of radius .

EP31:  Prove that the generating function of the circular billiard table is , and describe the critical set in the  -plane.

EP32:  For the linear expanding map of the circle given by , locate all period-2, 3, and 4 points.

EP33:  Show that Proposition 7.1.3 holds for .

EP34:  For the hyperbolic linear map on the torus given by the matrix , draw the torus with its two canonical loops that correspond the edges of the unit square in , viewed as a fundamental domain.  Then carefully draw the images of these two curves under the toral map.  You may want to draw the images of the edges of the fundamental domain in  first.

EP35:  Again for the hyperbolic linear toral map given by the matrix , finding and counting the fixed points of the nth iterate of the map involved finding the preimages of  under the related map  (See the proof of Proposition 7.1.10).  These were the integer vectors lying inside the parallelogram , where  is the linear map of  given by the same matrix.  Do the following: 

a)   Use the construction of  to calculate the number of fixed points of the third iterate of the toral map. 

b)   Draw the parallelogram for  and mark all of the integer vectors in the image. 

c)   Use , as well as  and  to identify the points in the original fundamental domain that correspond to integer vectors in the parallelogram (These are the actual toral points fixed by the third iterate). 

EP36:  The book uses the fact that expanding maps of  are topologically mixing to show that they are chaotic.  Without using topological mixing, show that expanding maps of  are chaotic.

EP37:  Do the same as in EP34 to show that the hyperbolic linear map of the torus given by the matrix  is chaotic. 

EP38:  Show the cylindrical twist map from EP25b has a sensitive dependence on initial conditions but is not chaotic.

EP39:  For  and map such that  for all , show that any lift  also satisfies  for all .

EP40:  Show that an isometry cannot display a sensitive dependence on initial conditions.

EP41:  Calculate the  -capacity and hence the box dimension of the Cantor Set formed by successively removing the middle half of each subinterval of the unit interval at each stage.  

EP42:  Show that for a map  on the metric space , the  th orbit segment metric  defined in class is actually a metric.  Recall that for  a metric on , we have .