Math 110.106, Calculus I (Biological and Social Sciences)
Fall 2009 Course Lecture Synopses
http://www.mathematics.jhu.edu/brown/Fall09106.htm
|
MWF 10:00am
- 10:50am Bloomberg 272 |
|||
|
MWF 11:00am
– 11:50am Mudd
26 |
|||
|
403 Krieger
Hall |
|
||
|
410-516-8179 |
|
||
|
Office
Hours: |
M |
1:00-2:00 pm |
by appt. other times |
|
W |
1:00-2:00 pm |
||
|
Below is some basic information pertaining to the lectures of this course. I will update this page after each lecture or two to benefit both the students in their attempts to organize the material for the course, and the TAs so that they know what material I covered and how it was covered. Please direct any comments about this page to me at the above contact information. |
· Wednesday,
October 14: Here I spent all of my time in Section
4.7. In particular, I recalled some basic analytic and visual aspects of
inverse functions, like domains and ranges of the inverse function in relation
to the original function, what graphs of two inverses look like and such, and
focused on the equation involving the composition of a function and its
inverse. The two basic examples I used were
and 
on the non-negative reals, and 
and 
on the positive reals. I used the composition equation 
as a means to derive the formula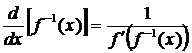 
, and to “calculate”
explicitly the derivative of the inverse, both for the known and then for the
unknown functions and later 
via a knowledge of 
. I also talked about
the pattern found in writing out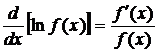 
,
and after an example or two, used it to answer the question: What is the function whose derivative is 
? This is a precursor
to the idea of anti-differentiating later.
· Friday,
October 16: Today I continued the discussion in Section
4.7 by talking about the inverse trigonometric functions, using 
(or 
) as my primary example.
The function is identical to the equation 
, and if we consider this last equation where y is an implicit function of x, then we can differentiate both
sides. This helps us discover the
derivative of through a bit of manipulation and calculation. The final result is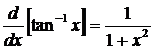 
. For HW, I will ask
that this calculation be repeated for the function
. Although now I see
that it is the arcsin function that is Problem #22 in
the text. So I will assign that one
instead. I also developed the idea of
calculating the derivative of certain kinds of functions via logarithmic
differentiation. The pattern found in
the derivative of 
, namely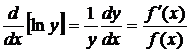 
, is very useful when confronted with functions that have the
following patterns: 1) where the
variable appears in an expression both in the base of the expression and in
it’s exponent, like 
(did this one explicitly) and 
(which I just mentioned), and 2) where the function is a
product and/or quotient with a lot of factors, like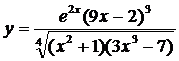 
. The reason is that
logarithms are quite good at allowing one to take a variable out of an
exponent, and also that the logarithms of a product (or quotient) is simply a
sum (or difference) of logarithms. I did
the last function explicitly in class.
· Monday,
October 19: In this lecture, I talked about how the
tangent line of a differential function at a point can serve as a good
approximation of the function near that point.
In fact, the linear function which serves as a tangent line
approximation is the best linear approximation to the function at that
point. This is because, as a line, it
has the same value and the same derivative of the function there. The two examples I used were to find ways to
estimate numbers like 
and 
without using a
calculator. The set up was to use 
and 
and find their local
linearization respectively at 
and 
. This was the first
half of Section 4.8. I will not cover
the second half of this section, and passed up on any real discussion of the
error incurred in approximating this way.
It would be best to talk about just how good an approximation a tangent
line will be when we know more about second derivatives and such. Instead, I moved into Section 5.1 and the
definitions of global and local extrema.
With a general discussion of global extrema and many visual examples of
functions that do and don’t have global extrema on chosen domains, I stated the
Extreme Value Theorem and talked about why all of its premises are
necessary.
· Wednesday,
October 21: Today, I continued the discussion on global
and local extrema with a determination of where a global extremum would occur
on a closed interval. Fermat’s Theorem tell us that at all extrema found on the inside of a closed
interval and where the derivative is defined must have derivative 0 there. Hence good places to find global extrema of a
differentiable function are places where the derivative vanishes. Global and local extrema can also occur at
places where the derivative is not defined (for example, at the corners of the
graph of a function). Places of a
function where the derivative either vanishes or is not defined are called
critical points and global extrema of a function on a closed interval occur
either at the endpoints or at a critical point.
I finished with a discussion of Rolle’s
Theorem in both lectures, and the Mean Value Theorem (MVT) in the early
lecture.
· Friday,
October 23: I detailed the Mean Value Theorem in the
second lecture, and then spent time in both classes explaining via examples of
functions like the absolute value function that differentiability of a function
on the open part of an interval is necessary for the MVT to hold. Then, I actually constructed the graph of the
Bertalanffy equation from its constituent parts, and discussed its properties
as a lead in to monotonicity, giving the definition for a (strictly) increasing
and decreasing function and the Monotonicity Criteria. I explained with use of the example the
function 
that the converse of the Monotonicity Criteria is not true (a
function can be increasing, for example, while its derivative can vanish at a
point). I gave many examples, graphed
the function 
directly above its derivative 
to show how the graph of the derivative of a function relates
to the graph of the function, and ended with a re-analysis of the von
Bertalanffy equation, how one can derive the graph from the information in the
function, without using a graphing device.
· Monday, October
26:
The main topic of discussion today was the concavity of a function which
is twice differentiable on an interval.
Using the Monotonicity Criteria as a guide (If 
on an interval, then 
is increasing on that interval), I showed that the same
statement can be made using sign of the second derivative; If 
on an interval, then 
is increasing on that interval, and how this relates, in
turn, to the “bending” of the function. This lead to a
working definition of concave up and down, and a multitude of examples of how
the basic functions behave (quadratics, exponentials, logarithmic functions,
the trig function 
, the cubic 
, a rational function like 
, etc.) in terms of concavity, as well as the earlier
derivative information. To relate this
all to the idea of finding local extrema, I explicitly related the following
three ideas: 1) a continuous function
has a local minimum at a point c if
the function is falling before it reaches c
and rising after it leaves c, 2) a
function differentiable near c (except
possibly at c) has a local minimum at
c if the derivative is negative
before c and positive after it (if is differentiable also
at c, then
),
and 3) a function twice differentiable on an open interval including c has a local minimum at c if and 
. Thus the derivative
is increasing as one passes through c. Next class, I will relate this last concept
to the graph of near one of its roots.
· Wednesday,
October 28: Today, I started with the Second Derivative
Test for Local Extrema. Basically this
is the formal conclusion of part three in the last lecture. I showed by example that when both the first
derivative and the second derivative are zero at a critical point, the test is
inconclusive. The three examples 
and 
illustrate all three types of possibilities under this set of
conditions. Then I played around with
finding the global extrema of the (not so easy to imagine) function 
on the interval 
. The only critical
point is a zero of the derivative, and the function is positive except at 0, so
the global min is easy to find. The
global max, however, is either 
at 
, or the other end point 
at 
. Hard
to see without a calculator.
However, since by the Second Derivative test, is a local max, and there are NO other critical points, the
other end point value must be smaller (why??).
Then I defined inflection points, and spent time specifying that an
inflection point only can occur at a place where the function is continuous, and the concavity changes across the point. Asymptotes cannot be inflection points, but
corners can. Lastly, I defined and
worked with horizontal and vertical asymptotes.
· Friday,
October 30: Continuing the above discussion, I talked
briefly about inclined asymptotes, following closely the book’s example. I will not work much with this topic, but
wanted everyone to understand well the discussion in the book. Then I went into a very detailed curve
sketching problem after summarizing all of the function feature data we have
been working with over the last two weeks.
The function I sketched was 
, which displays a lot of interesting behavior. Then I went into the section on Optimization,
setting up four simultaneous problems based on applications. The first is the Ricker curve, first seen in
Problem 64, Section 4.6, and due this week.
The function is 
, which when we set 
IS the function we just talked about in the last
lecture. I gave a treatise on where this
function occurs in population dynamics and why it is interesting, and stated
the optimization problem: Fund the adult
population P in a fish stock which
maximizes the potential growth of the next generation fry 
. The interval is 
, so verifying that the function even has a maximum is
necessary. The second is Example 2 in
this section of the text. The third is
to enclose a rectangular field of maximal area using 1200 feet of fence where
one side, adjacent to a river, need not be fenced. The fourth is to minimize the amount of
material needed to enclose 1 liter of fluid (1000 cubic centimeters) in a
cylindrical can with a lid. IN all four
cases, I talked my way through the idea that these problems are well-defined
and that the functions will indeed have the appropriate extremum. And I talked about how in the last two
problems, the function one seeks to extremize starts
out as a function of more than one variable, and hence some care is
needed. In each of these latter cases,
there is other information in the problem and one can find a secondary
relationship between the two variables that can serve to make the problem look
more like a standard problem. I will
solve all four of these in the next lecture.
· Monday,
November 2: Continuing the final topic in the last
lecture, I restated the four problems above and in turn solved each of them in
detail. I spent time detailing the
patterns that emerge in all of these and other similar problems, and laid out a
general strategy for solving optimization types. The only troubling aspect of optimization
problems is when the interval in which you are seeking to optimize is either
open, or of infinite length. In this
case, instead of checking the endpoint, one must seek the limiting behavior of
the function to ensure an extremum exists and wher it
may lie. Three of the four examples
above had infinite length intervals. The
first was a particular problem, as we have no real machinery yet to calculate 
. This is the proper
segue into the next section on L’Hospital’s
Rule. I gave some background, using
rational functions, on what constitutes an indeterminate form.
· Wednesday,
November 4: Today, I defined L’Hospital’s
Rule, and discussed both its utility and the precise nature of the conditions
in which is applies. I also gave an
intuitive idea for why it works. Then I
went over many diverse examples of using it in practice. The two standard indeterminate forms (remember,
these are not mathematical expressions, but simply symbolic notation to
indicate the type of situation for which the rule may apply), of 
and 
may
also appear in other forms:
, 
, 
, 
, 
and 
. I went over these,
both by discussion the nature of the indeterminacy and via examples, and
discussed ways to manipulate the function in the limit to make it look like one
of the two that are detailed in the rule.
More examples were worked out.
Specifically, I worked out the example that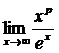 
=0
for any natural number 
by
a study of the patterns that emerge as one increments p.
· Friday,
November 6: Here I motivated the discussion on antiderivatives
by talking about the Newtonian equation 
as well as basic differential equations. Going backwards form a function’s derivative
back to the original function is not so straightforward, and there are few
rules. It is more pattern
recognition. After a detailed definition
of an antiderivative, I mentioned that some functions have antiderivatives that
are not easy or impossible to write simply.
I mentioned that there are always many antiderivatives for any function
which has one, but they all differ by a constant, and that the general
antiderivative of a function is a of any particular antiderivative and an
arbitrary constant. I used a graphical
example of a function 
and its general antiderivative 
to illustrate. I also
talked about the idea of finding a particular antiderivative of a function by
finding the general antiderivative and then using one known value of the
antiderivative to “solve” for the constant C. This is the same as the notion of an Initial
Value Problem in Differential Equations.
I then detailed some of the more obvious patterns in functions that
allow for easy recognition of their antiderivatives, like power functions, the basic
trig functions and exponential functions.
· Monday,
November 9: This class started with a detailed
calculation of the antiderivative of the function 
on its full domain.
Then I talked about Newtonian physics and used the example of a ball
thrown directly up into the air to show that one can recover the function of
position of the ball with respect to time knowing simply the acceleration due
to gravity. I ended this discussion with
a specific example. I then discussed the
idea of calculating the area between a positive function and the x-axis on a closed interval when the
function is constant or piecewise linear, and what happens when the function
graph is curved. To understand better
the latter, I talked about the idea of estimating the area by rectangles of
equal width and using the function to generate rectangle heights, and how the
estimate would get better with a larger number of thinner rectangles. I then analyzed the notion of what would
happen should the rectangle widths get vanishingly small (so that there are a
large number of them), and what would happen in the limit. I also studied the idea that the choice of
heights of each of the rectangles does not need to be well-coordinated, and
that the width of the rectangles does not need to be the same. But care should be taken in how we define the
rules for estimation.
· Wednesday,
November 11: Today, I moved past the general idea of
calculating the area between a curve given by a function on a closed interval
and the x-axis and defined the
definite integral. After going over the 
-notation and the idea of a partition 
, with its norm 
, I defined the definite integral of a continuous function on
a closed interval as a limit of estimates of the area “under a curve” by
Riemann Sums, where each estimate is given by a partition, and the partition
norms tend to zero. This is rather
abstract outside of the interpretation of area, but will become clearer in
time. I talked about the interpretation
of area when the function lies below the horizontal axis, what the symbols mean
in a definite integral, and the kinds of functions that are integrable
(the definite integral exists). Next I
will detail many of the properties of the definite integral, and reinterpret
the integral in terms of the differential calculus.
· Friday,
November 13: Here, I worked through many of the properties
of the definite integral of a continuous function over a closed interval. Then I introduced the function 
defined when 
is continuous on an interval 
. I discussed its
properties and its interpretation in terms of area between the graph of
and the t-axis from
a to x.
I then asked if it is a differentiable function, and calculated its
derivative using the definition of the derivative. This leads to the conclusion that 
, and the Part I version of the Fundamental Theorem of Calculus. One useful interpretation that comes directly
from this is the notion that integrals and antiderivatives are related, and
that the derivative of a function defined by an integral winds up being the
integrand. That differentiation and
integration are inverse operations. I
finished with a few calculations like this, using the function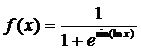 
, taking the derivative of the definite integral of this
function when the upper limit is simply x,
when the upper limit is an unknown 
and
when both the upper and lower limits are and
,
respectively. This leads to the Leibniz
Formula, which I stated.
· Monday,
November 16: Restating the Leibniz Formula as a lead in to
today’s lecture, I defined explicitly the indefinite integral, which is the general
antiderivative of a function, using the integral notation. I stated its properties in contrast to the
definite integral, and worked a few examples of some of the basic functions. Mentioning that we have worked out a lot
without any real discussion about just how to “calculate” a definite integral,
I used the antiderivative 
and a second antiderivative 
, where 
(this is directly in the book), to develop the equation defining
the Fundamental Theorem of Calculus Part II, namely 
, where again is ANY antiderivative of . I worked through a
few examples to show how straightforward a calculation like this is. Then I introduced the first application of
integration we will use; to find the area of any region in the plane that can
be described as bounded by curves expressed as functions.
· Wednesday,
November 18: Continuing the discussion on applications, I
worked out more examples of calculating areas of regions in the plane when they
can be expressed as lying between two expressions as functions of either x or y. Then I moved into the second area of
application using the Fundamental Theorem of Calculus. Here, one can calculate the cumulative change
in the value of a function over an interval by integrating its derivative over
that interval. I set up the problem as
one of recovering distance by integrating velocity with respect to time. On the level of Riemann Sums in estimating
the integral of velocity, each Riemann sum box would have sides which would
look like a small interval in time along the bottom, and height which would be
the velocity value at some point in the time interval. The area of this box, as an approximation to
the integral, is length times height, or (time) multiplied by (distance over
time), resulting in only distance. As an
example, I worked out a specific application, where if one measures the speedometer
reading at every moment of a road trip, then one can use the definite integral
of this velocity to recover how far the trip was. In my case, I used a quartic
for velocity and recovered a 6 hour road trip that took the driver over three
hundred miles.
· Friday,
November 20: Today, I finished the discussion of
applications of the integral with a relatively brief development and example of
the average value of a function. This
topic is quite straightforward, and the discussion was basically one of visual
identification (I used the analogy of a function over a closed interval looking
like a snapshot of the surface of a water tank mid-wave. The average value of the function over that
interval is sort of like the level of the water after the wave dissipates and
the water becomes calm. I then moved
into chapter 7, and discussed the notion of using patterns to recognize the
antiderivatives of complicated functions.
The first is an integrand that looks like a Chain Rule derivative. The motivation for this was the calculation for 
. Writing this out
using 
and 
, we can rewrite the previous expression as 
which is equal to 
where 
is the antiderivative of 
. More generally, given 
, one can use a substitution 
to untangle the last integrand, and get 
, where and 
. I cautioned that this
last expression is not technically identical to the expression
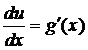, but there is a well defined notion of the differential of u and its relation to the differential
of x.
This provides a method for calculation.
When one can recognize the integrand as a product of a composition of
two function and the derivative of the inside
function, then one can make a substitution to simplify, or untangle the
integrand, making it easier to calculate.
I did a couple of relative easy examples.
· Monday,
November 23: I finished the discussion on the Substitution
Rule today (or rather, the Anti-Chain Rule), by looking at ways to recognize
the patterns in the integrand of an integral that indicate that a substitution
would be helpful. The obvious one above
is a start; when
the integrand includes a product of functions, where one factor is a composition
of functions and the other factor is the derivative of the “inside” function of
the composition. I talked about
variations of this theme. A second pattern
is when the integrand would be much easier to find the antiderivative of if the variable
were translated (the substitution here would be something like 
). This works well in
instances like 
or 
, where after the substitution, the integrand becomes simply
a sum of power functions (work this out).
The last is rather like the first; when the integrand has the form 
. After the
substitution, the antiderivative becomes 
I talked also about the
definite integral version, how one can use the substitution to change also the
limits. IN this case, there is no need
to return to the original variable, and did a few examples.
· Monday,
November 30: Today I introduced the technique called “Integration
by Parts”, where one can use a double substitution to rewrite the integral in a
way facilitating a solution. Another
name for this might be the “Anti-Product Rule”, since this technique is derived
from the product rule in differentiation, and in essence, recognizes the
pattern found in the rule. I derived
this rule from the product rule directly, and talked about its structure. The quintessential example of an
antiderivative found via this technique is 
. The proper substitution here is 
, and 
. Then one can calculate 
, and 
, and the rule says that 
. The rule is
typically written 
to facilitate the double substitution of u and the differential of v. And the right hand side is, hopefully, includes
an easier integral to solve. This
technique works well when the integrand is a product of functions where one is
a polynomial and the other has an easy antiderivative to find, or when there is
a single function which is hard to integrate, but whose derivative multiplied
by x is easy to integrate. I did examples of each type, as well as an
example of the definite integral version.
I ended with an example of a way to find the antiderivative of 
,
by using this technique twice and then solving for the unknown integral.
· Wednesday,
December 2: Last class, I did a brief introduction to a
technique for finding the antiderivative of a rational function. Every rational function can be rewritten as a
sum of a polynomial and a proper rational function. In turn, every proper
rational function can be written as a sum of proper rational functions, where
each denominator in the summands is a factor of the denominator of the original
proper rational function. This sum is
called a partial fraction decomposition, and the
factors are all either linear or irreducible quadratic. I presented the technique for performing the
decomposition via knowing the denominators and using a set of unknowns for the
numerators. Solving for the unknown
numerators is algebraic, and each of the resulting partial fractions is easy to
integrate. I did a few basic examples,
and passed on any difficult cases. I
ended this session with some talk about the exam on Friday and beyond.