


|

|
What is complex analysis?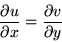 and and 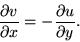 , called the Cauchy-Riemann equations.
These two equations together imply that complex-differentiable functions are
very special. In particular, they preserve angles (which makes them useful in
modelling fluid flow), and have harmonic real parts (which makes them great
models for temperature fields). , called the Cauchy-Riemann equations.
These two equations together imply that complex-differentiable functions are
very special. In particular, they preserve angles (which makes them useful in
modelling fluid flow), and have harmonic real parts (which makes them great
models for temperature fields).
One difficulty of reasoning about functions from the complex plane to the complex plane is that their graphs should be drawn on a four-dimensional space (two for the domain, and two for the range), but that's impossible. Modern physics gives us strong empirical reasons to believe that imaginary and complex numbers do indeed exist, whatever that means. The tools developed in this course have very "real" applications, especially in quantum physics, despite our tendency to call them "imaginary"!
|
This page last modified Fri Sep 10 14:52:21 2004
Questions? Comments? Please send feedback to jason howald:
![]()